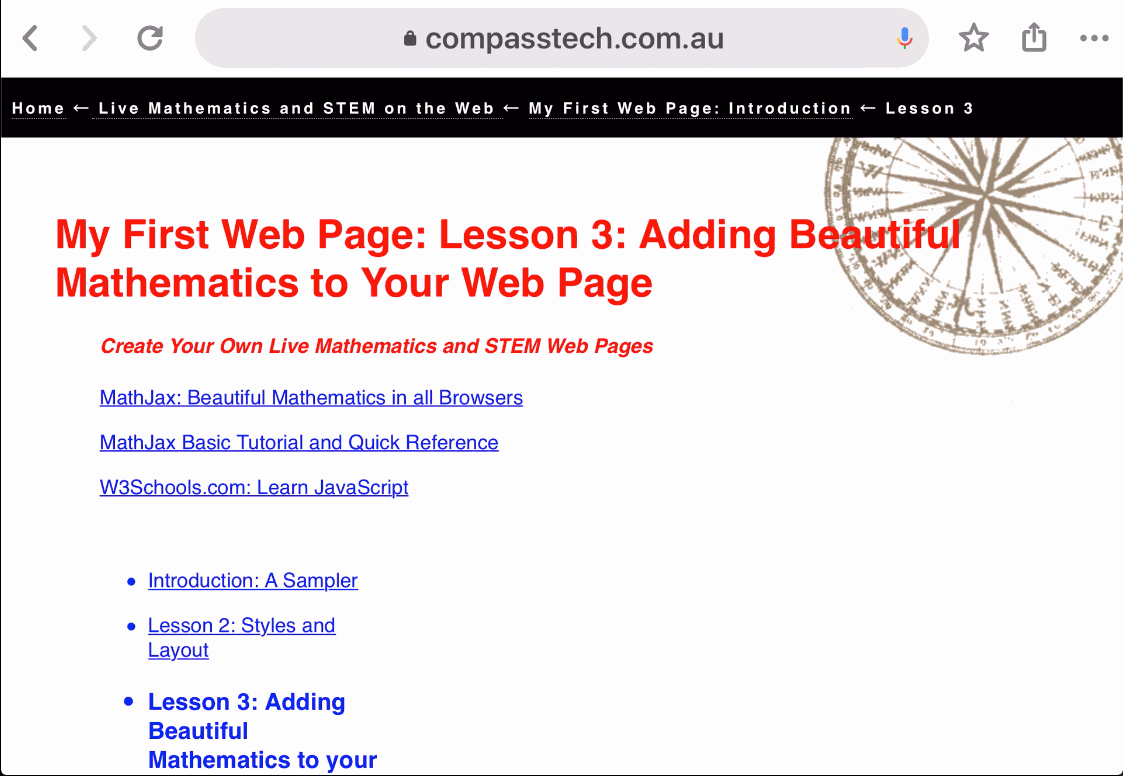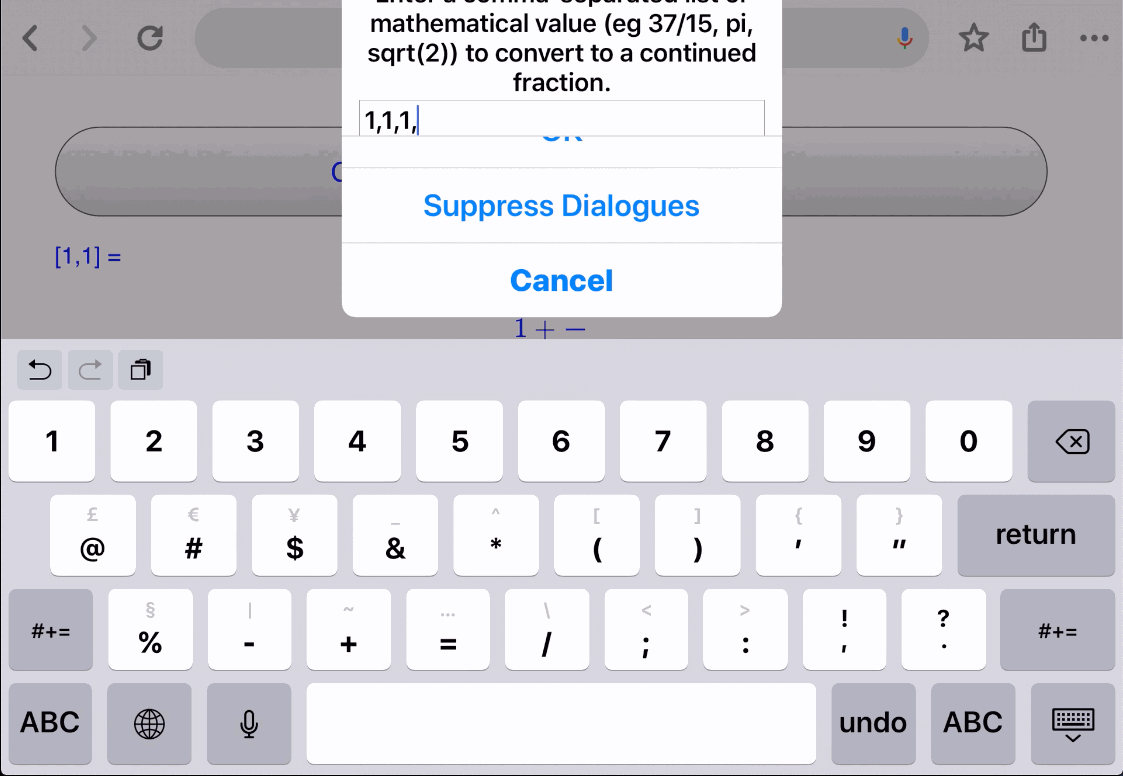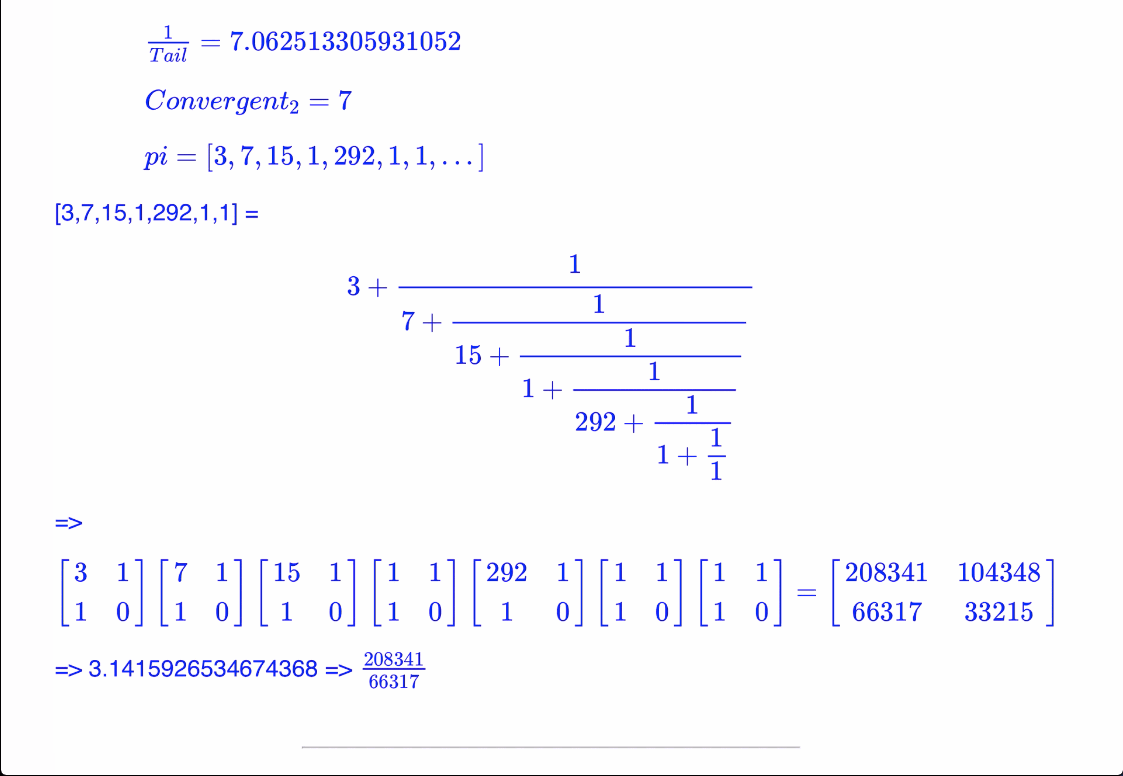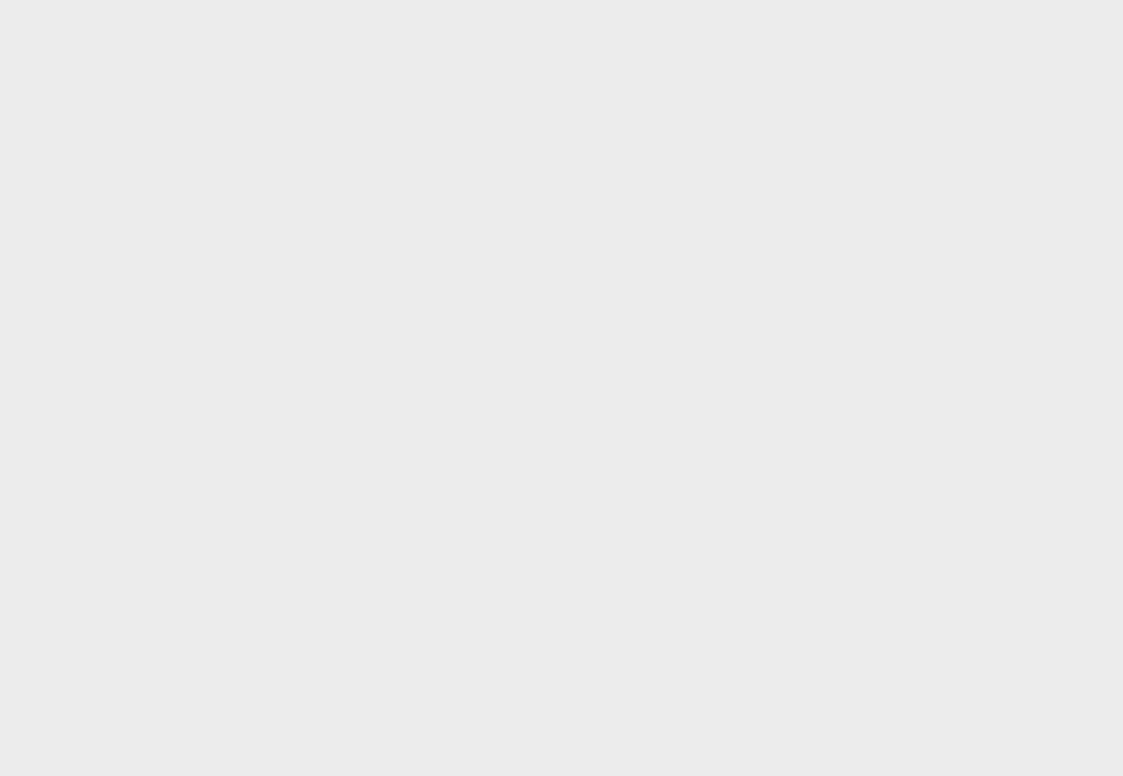
The focus of this series of lessons is on learning to create live web pages based upon two key elements: mathematics (in particular) and STEM (in general). While we have seen that it is relatively easy to add text of all sorts to your web page using HTML, mathematical notation, unsurprisingly, presents its own very special set of problems.
From my early experience of web coding (over 20 years ago), I have some memories of MathML - and remember it as being pretty complicated. Today, we have much better solutions - in particular, MathJax, a JavaScript library which takes the hard work out of representing even complex mathematics in a beautifully elegant way. For (relatively) simple live entry of mathematical forms, there is also MathQuill, offering students immediate feedback that they are entering their mathematics correctly. Together, these JavaScript libraries support both input and display of mathematics in correct notation.
The key consideration lies in how students best learn algebra.
Appropriate technology offers huge advantages for increasing student understanding and manipulative skills, and opportunities for exploration, but one cautionary element lies in the representation of algebraic forms - computers are much more comfortable with elements of the form
x = (-b + sqrt(b^2-4*a*c))/(2a)
whereas we expect our students to work with and understand something more like \[x = {-b \pm \sqrt{b^2-4ac} \over 2a}\]
If the focus of our instruction is on coding and learning to work with technological tools, then the first form is appropriate and, indeed, necessary.
But if the focus is on the mathematics, then we do not want to put further obstacles between the students and the mathematics that they are trying to learn. Input and output of the mathematics must both be considered when choosing appropriate technological tools.
If those tools are web-based, as we are suggesting in these pages, then we must make every effort to make the mathematics as accessible as possible, and for that reason, it is of great value to learn how to present our mathematics in correct form where possible.
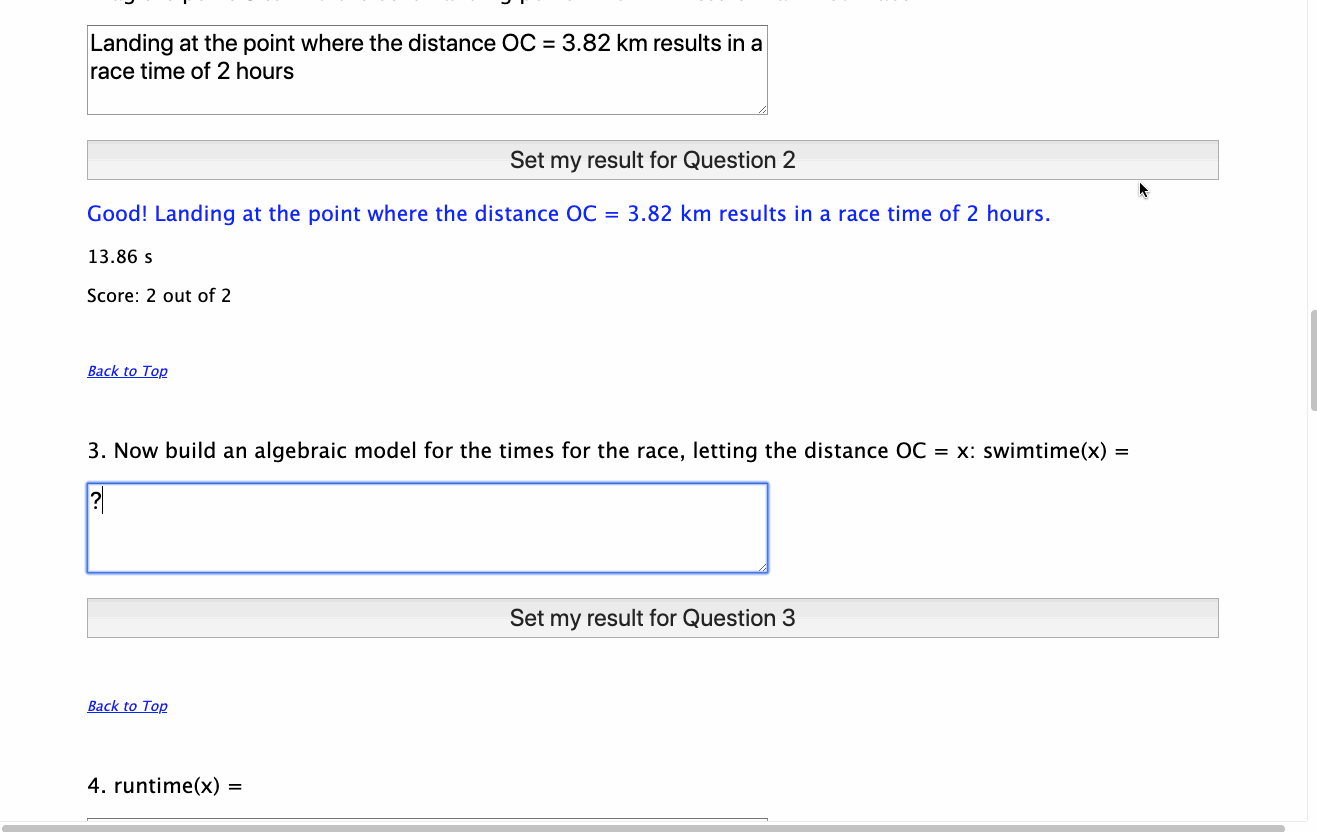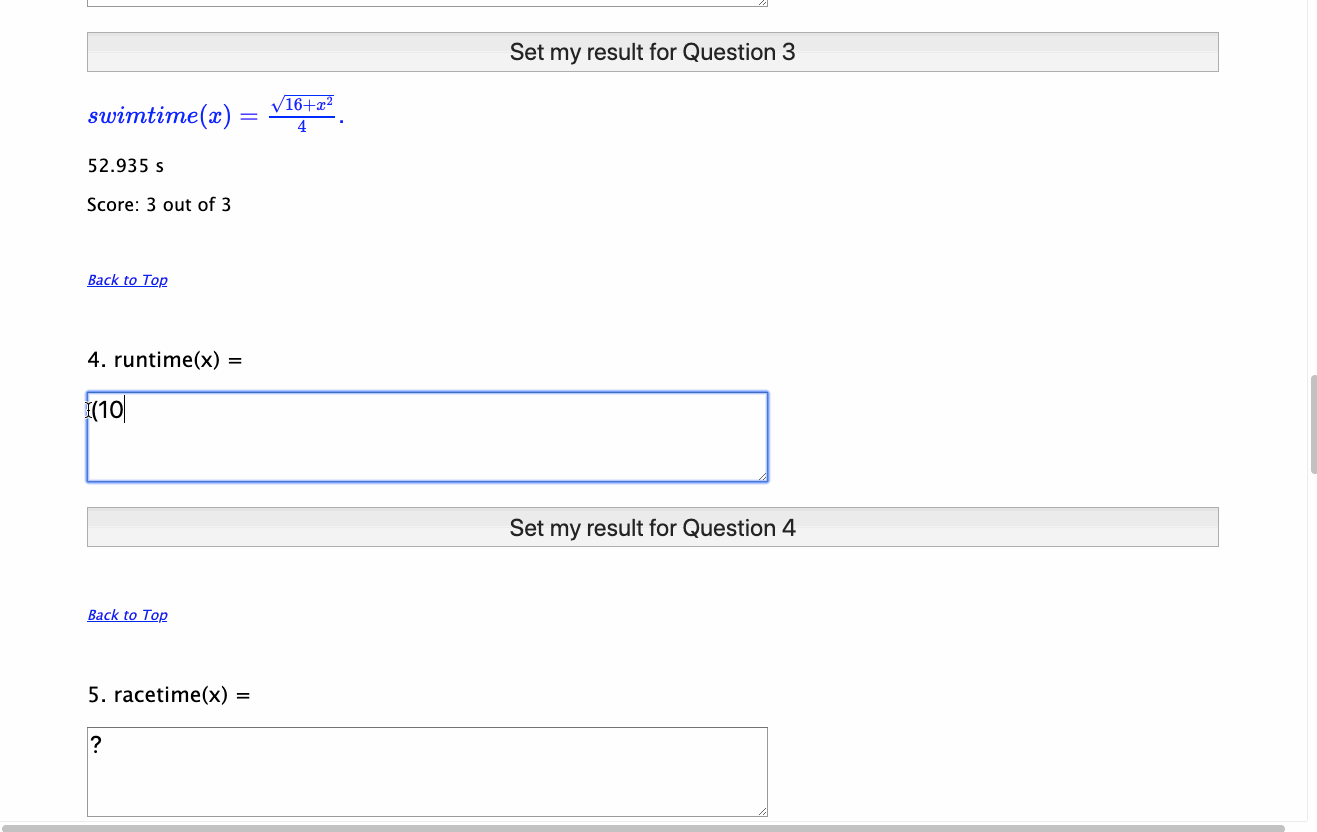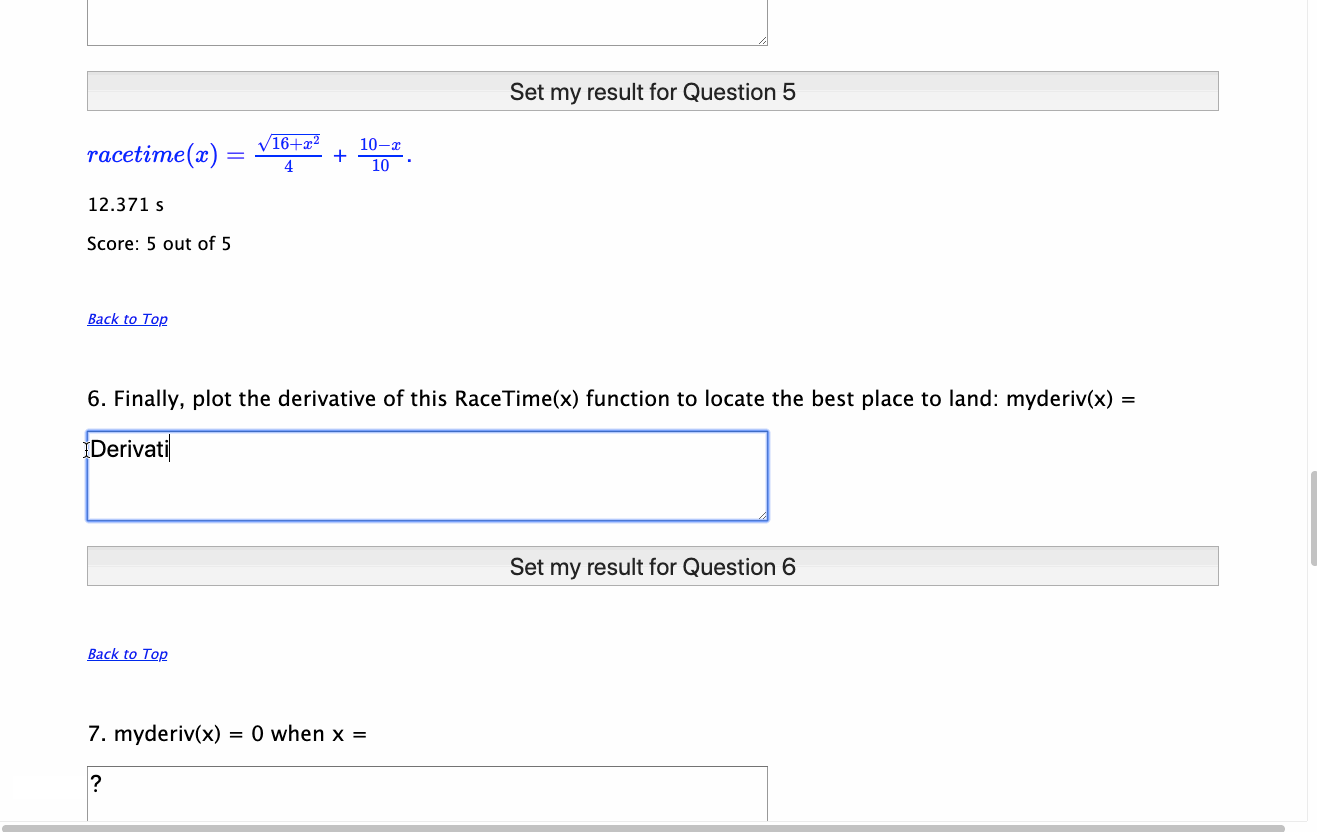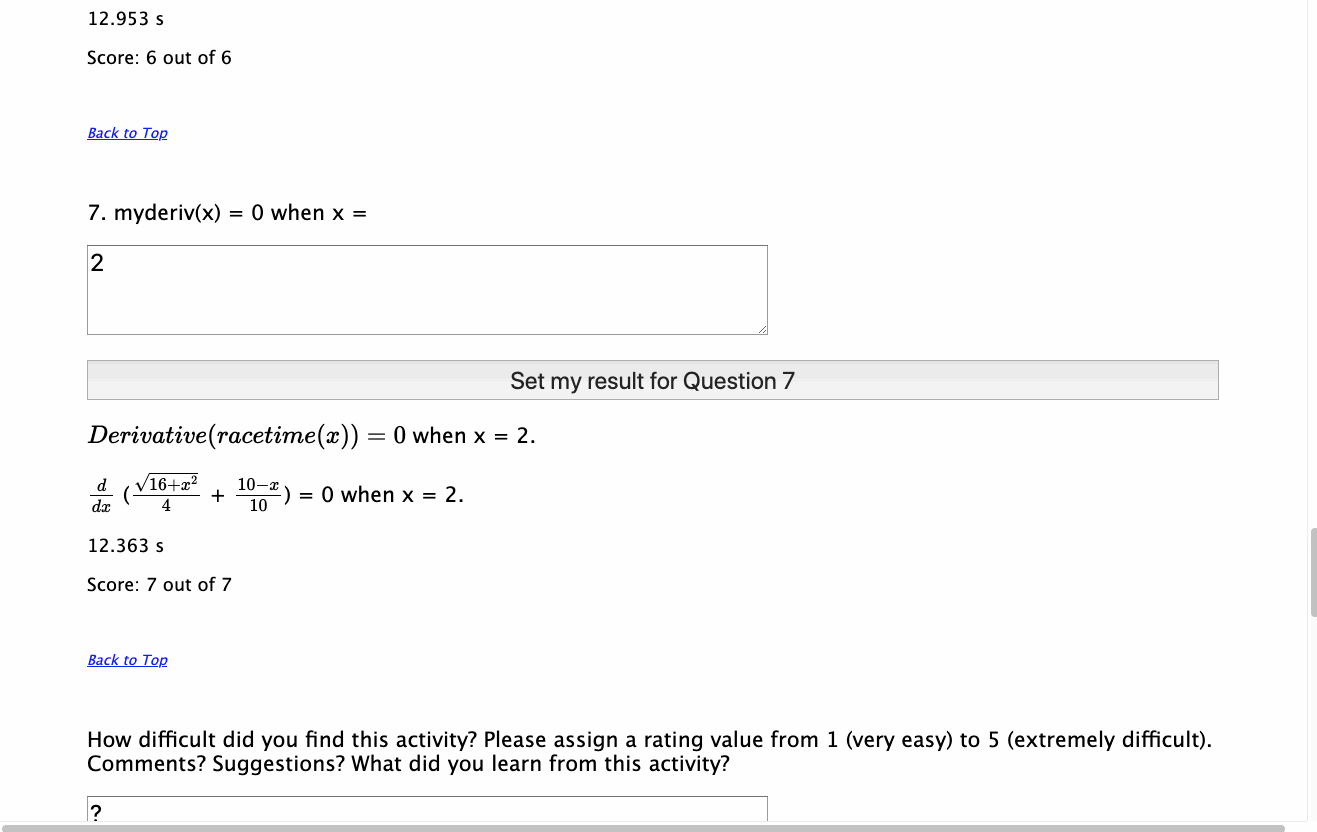
For examples of just what this might mean, you might take time to explore the examples developed in the GeoGebra Assessment Showcase on this site - you will see two key elements linked to this discussion:
Input, where possible, takes place using correct mathematical notation and real language - define functions for base(x) and height(x) and then the area of the triangle is defined as \({{1} \over {2}}\cdot base(x) \cdot height(x)\). Consider the power of this real language approach, made so much more accessible through the use of technology - and computer algebra in particular.
Output is represented using both real language functions (where these exist) and correct mathematical format, using MathJax, allowing students to visually link the various representations being explored.

If you have any questions or would like to share your experience with this utility, please drop me an email!
Back to Top