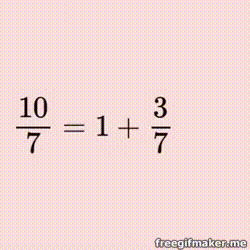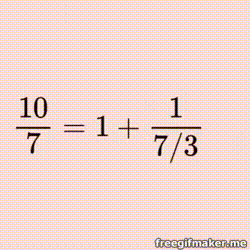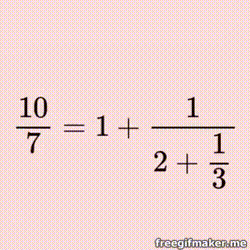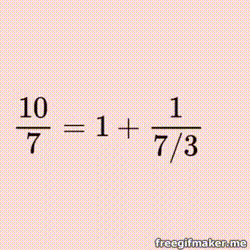©2021 Compass Learning Technologies → Live Mathematics on the Web → GXWeb Showcase → GXWeb Jigsaws and Quizzes

GXWeb Jigsaws and Quizzes

Symbolic computations on these pages use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb

Saltire Software, home of Geometry Expressions and GXWeb

YouTube Introduction to GXWeb Jigsaws (6:46)

AAMT eConference Presentation 2021: GXWeb and Jigsaws: Free Online Tools for Exploring Beautiful Mathematics (37:30)

 
 

Fancy some mathematical fun?

Use jigsaws and GXWeb to explore some mathematical gems drawn from geometry, number theory and elementary algebra - and then follow the links provided to see some of their many and varied applications!

 

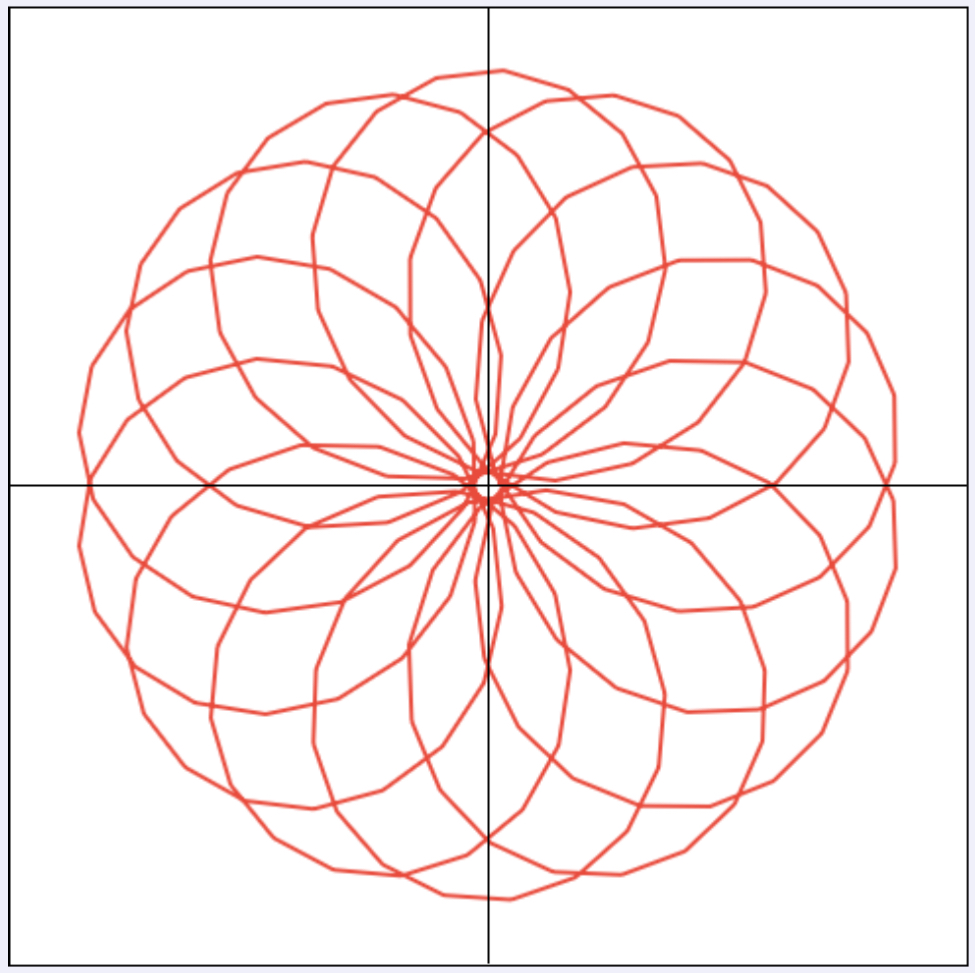
Create Your Own GXWeb SpiroGraph

Back to top

The spirograph is a geometric drawing device that has been a source of interest and fun for young and old for some two hundred years!

But have you ever thought of designing your own spirograph?

The amazing free GXWeb software makes creating all manner of beautiful geometry easy, and the spirograph is no exception!
 

GXWeb Polygon Playground

Back to top

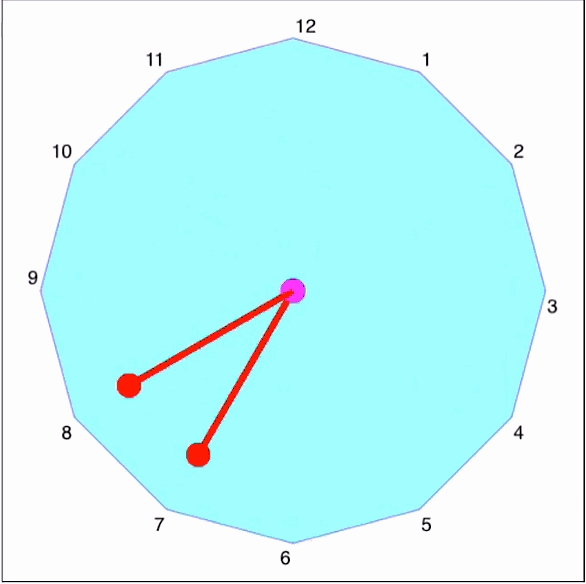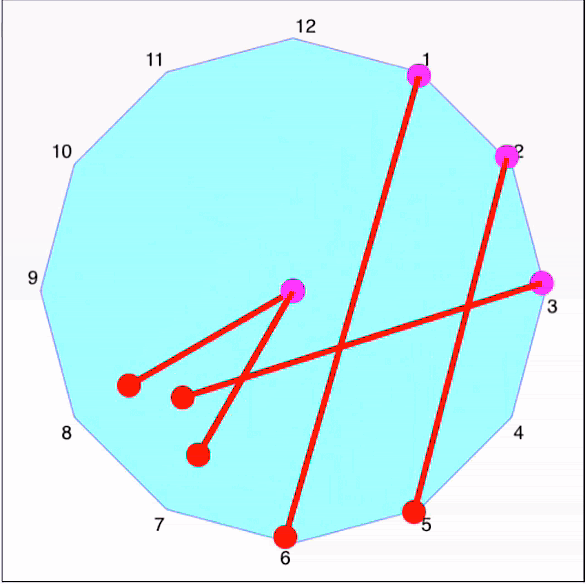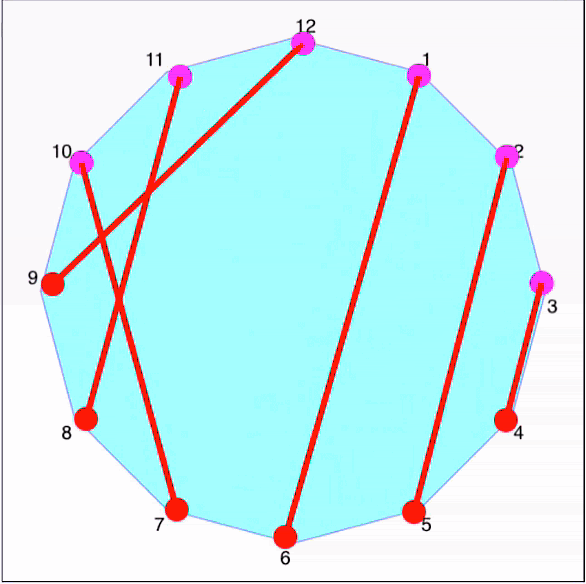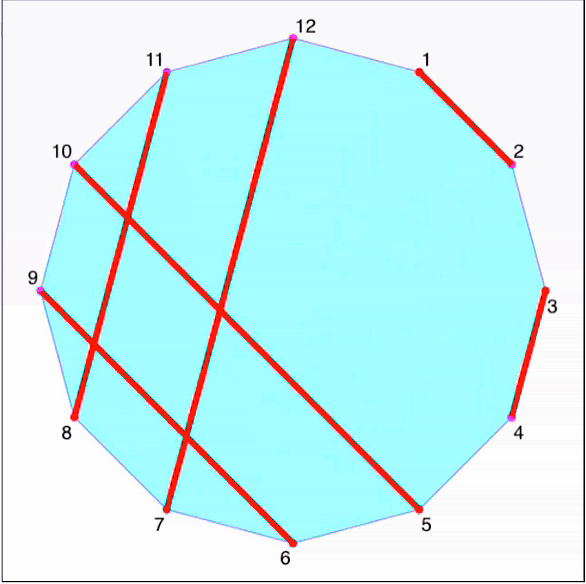
Two teams (A and B) of \(n\) players each are seated around a \(2\cdot n\)-gon polygonal table. Team A are allocated the odd-numbered seats, and team B, the even numbers.

How do we set up the draw so that each member of team A competes against each member of team B exactly once?

How many times must they meet?

Alternatively, consider a clock face with \(2\cdot n\) "hours" marked around the dial.

Let \(a(n) = \) number of ways to match the even hours to the odd hours, modulo rotations and reflections.

OR...

Given a \(2n\)-gon...

You are to drag \(n\) diagonals so that they don't share end points, and there are an odd number of polygon sides between the end-points.

How many such variants do you think exist for a hexagon? For an octagon, decagon - or the standard clock dodecagon?

Why stop there?

Play! Try your own! Browse the examples - and then try the Polygon Quiz!

 

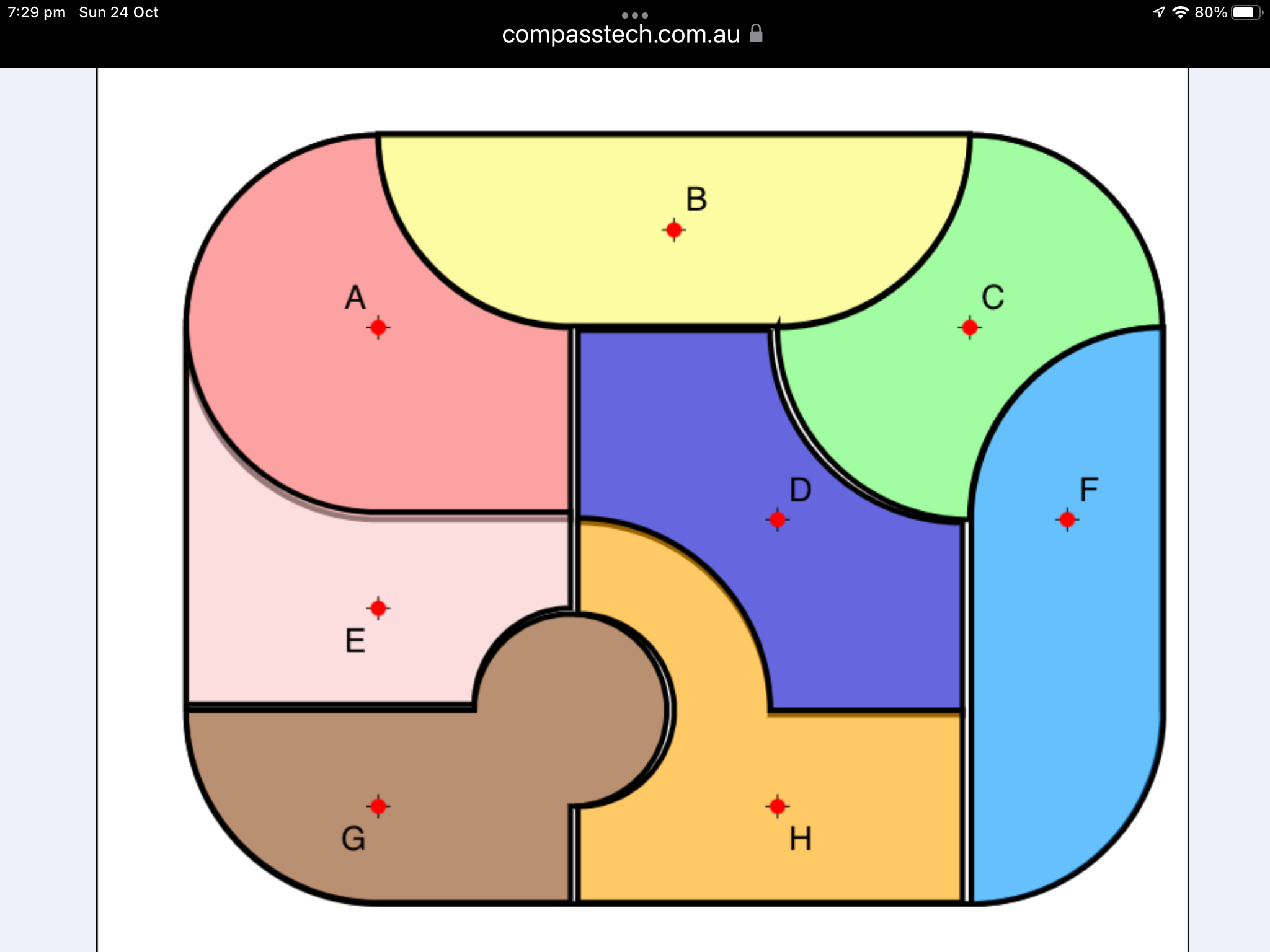
TakTiles Jigsaw

Back to top

Tak Tiles were designed by Geoff Giles for the DIME (Developments in Mathematics Education) Project. This live web version supports three levels of interaction for students:

  1. Jigsaw Mode: A simple jigsaw puzzle for students to move the pieces into their appropriate positions.

  2. Exploration Mode: Students can select a shape and try dragging \(x\) and \(y\) tiles to match it - with the chance to display the current algebraic expression as they work. They can use check mode to verify their work.

  3. Challenge Mode: Working without a net this time, random tiles are offered, and students try to express each in terms of \(x\) and \(y\) - but without the displayed expression to assist them.
 

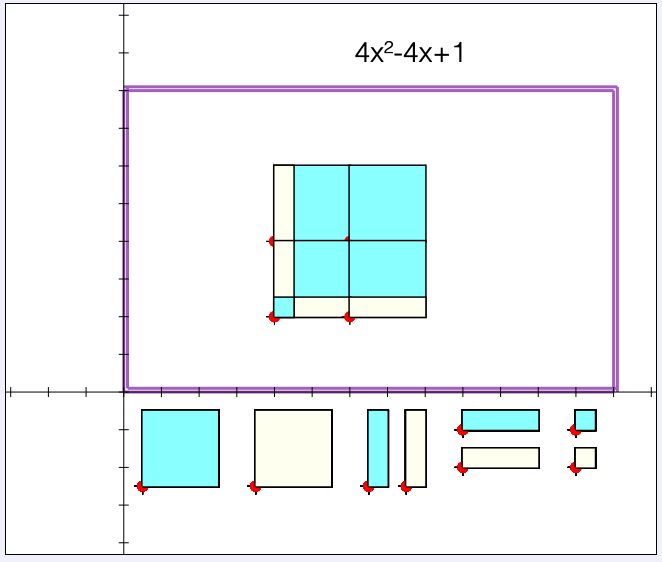
Algebra Tiles Jigsaw

Back to top

What does \(2x + 1\) mean to you? What about \(4-3x\) or even \(x^2=x+1\)?

What dominant image springs to mind?

Do you see an object or a process?

Do you think of a graph? A table of values?

Students who are successful in algebra tend to have a richer repertoire of images compared to those less proficient. As teachers, we need to build these images deliberately and with care.

Algebra tiles can be a powerful tool for building deep understanding, and the virtual variety actually offer some major advantages: they explicitly link the shapes to the symbolic form, and they establish that variables are dynamic rather than static things.

 
 

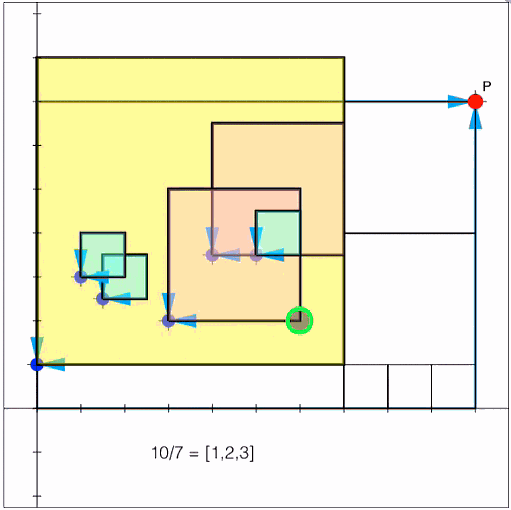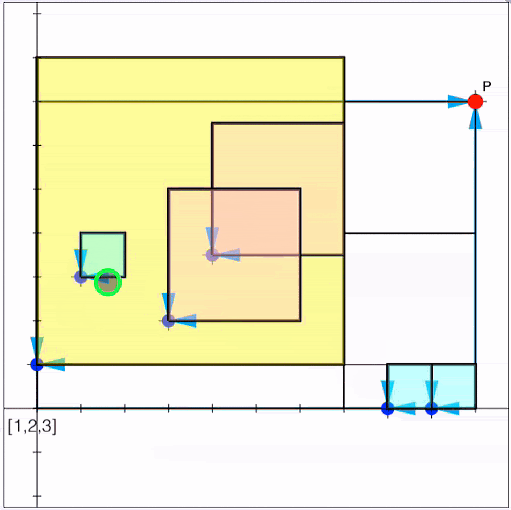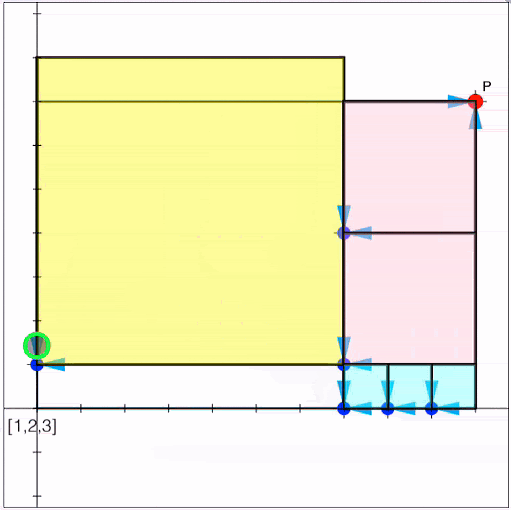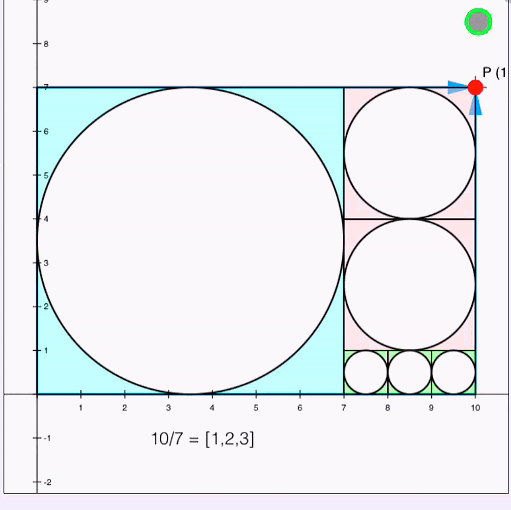
Fractured Fractions Jigsaw

Back to top

(Never heard of continued fractions? Tap here.)

Every real number, rational and irrational, can be represented by a continued fraction - the rational ones are finite, of course, but both finite and infinite offer some wonderful patterns and opportunities to explore!

Unlike irrational decimals, however, even irrational continued fractions can be predictable and are an ideal way to calculate approximate values - as accurately as you like!

See from the model that \(\frac{10}{7}\) becomes \([1,2,3] = 1 + \cfrac{1}{2 + \cfrac{1}{3}} \).

So what number gives the continued fraction \([1,2,3,4]\)?

Can you find some values whose continued fractions are composed entirely of the number 1?

  
 
 

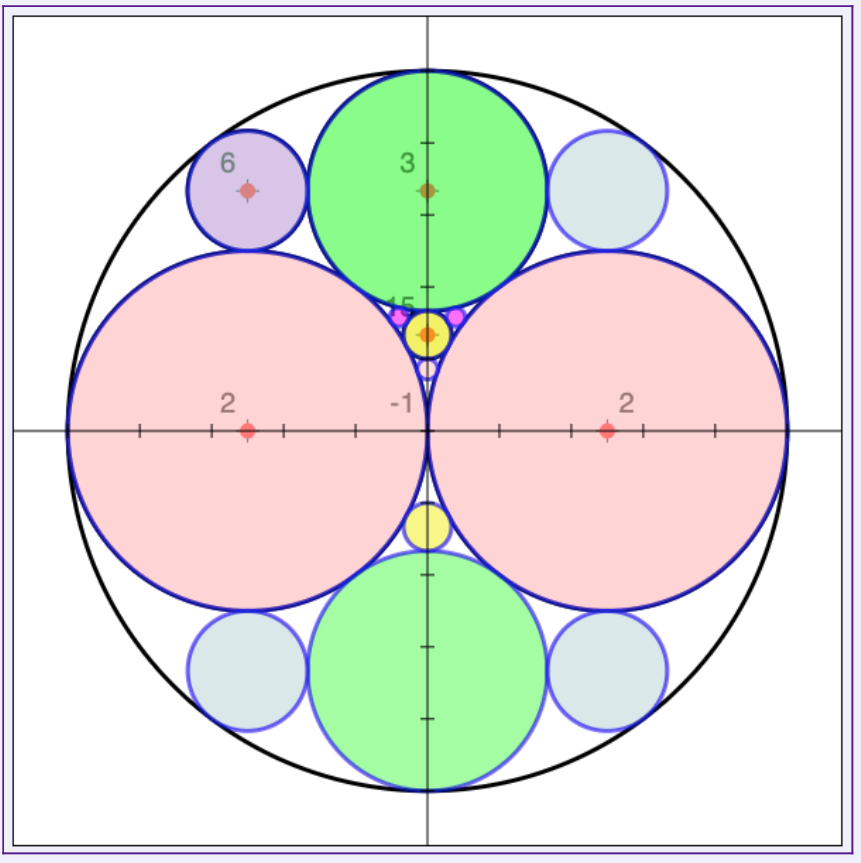
The Kiss Precise: Kissing Circles Jigsaw

Back to top

Given the sequence \([-1,2,2]\), what do you predict to be the next number?

And what might follow \([-1,2,3]\) - or \([2,2,3]\)?

What about \([-2,3,6]\)? Or \([-6,7,42]\)?

Each number refers to the curvature - or bend - of the circle it describes - which is the reciprocal of the radius. A negative bend describes the circle surrounding the others!

Here we imagine a shape (circle, rectangle, triangle(-ish)... even a Golden (Pappus) chain!) completely filled with bubbles - kissing circles!

Rene Descartes found the rule for such patterns, and it lay in a quadratic equation!
 
 

Fraction Trees, Farey Numbers and Continued Fractions

Back to top

Did You Know that Fractions Grow on Trees?

Or that (Fraction) Trees Can Grow from (Continued) Fractions?

Suppose you wanted to make a list of all the rationals... How might you start?

Can you see how the fractions at each level of our fraction trees are calculated from their parents?

How do the paths to each term lead to continued fractions?

And how can a special continued fraction lead to our fraction trees?
\[0+\cfrac{1}{3-\cfrac{1}{1-\cfrac{1}{3-\cfrac{1}{1}}}}\]
 
 

Construct your own Model with GXWeb

Back to Top

 
 

Behind the Scenes

Back to top

 
 

©2021 Compass Learning Technologies ← Live Mathematics on the Web ← GXWeb Showcase ← GXWeb Jigsaws and Quizzes