GXWeb Fractured Fractions Collection
Saltire Software, home of Geometry Expressions and GXWeb
Symbolic computations on this page use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb
An Introduction to Continued Fractions by Dr Ron Knott
Chaos in Numberland: The secret life of continued fractions by John D. Barrow
Explore Bill Gosper (1972): Continued Fraction Arithmetic
Calkin and Wilf (1999): Recounting the Rationals
Bruce Bates (2014): The Stern-Brocot Continued Fraction
Bates, B., Bunder, M. and Tognetti, K. (2010): Linking the Calkin–Wilf and Stern–Brocot trees
Welcome to the Fractured Fractions Collection!
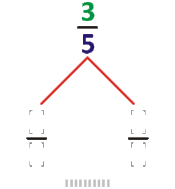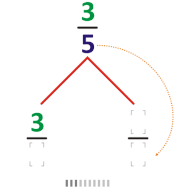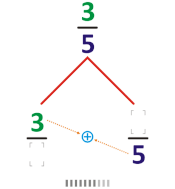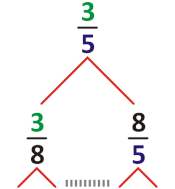
Try the Continued Fraction JigSaw! Just rearrange the squares to fill the given rectangle, and then press INPUT (or the JIGSAW button again) to enter your answer.
Then go on and explore some of the wonderful connections between continued fractions and some surprising and important corners of mathematics. Did you know, for example, that fractions grow on trees?
Then dig deeper into Continued Fractions.
With thanks to the late Dr Keith Tognetti for pointing me in the direction of continued fractions many years ago and igniting in me a life-long passion, and to Dr Bruce Bates (both of the University of Wollongong) for revealing to us all the beautiful Stern-Brocot Continued Fraction. With colleague Dr Martin Bunder they have brought to light many wonderful and often surprising connections between binary trees and continued fractions.
|
|
Introduction
If you have not come across continued fractions in your mathematical travels, then it is high time you did!
Every real number, rational and irrational, can be represented as a continued fraction. While normal fractions can only represent rational numbers, continued fractions are different - full of surprising patterns and relationships.
Not surprisingly, rational numbers produce finite continued fractions, while irrationals become infinite continued fractions.
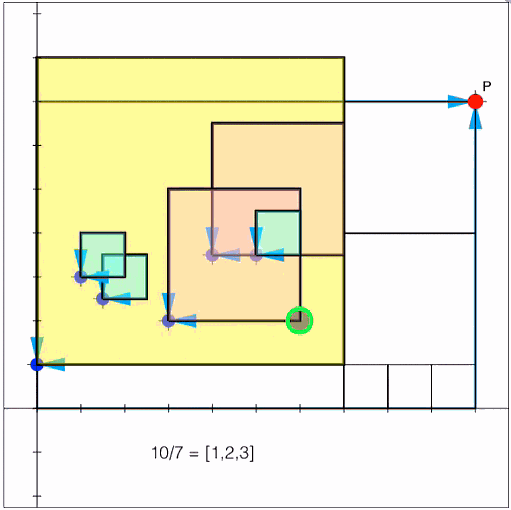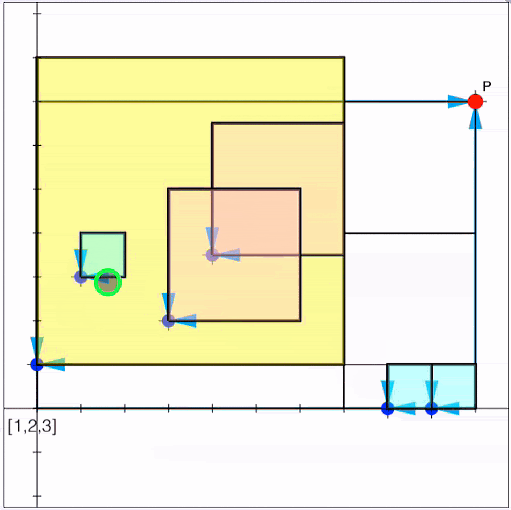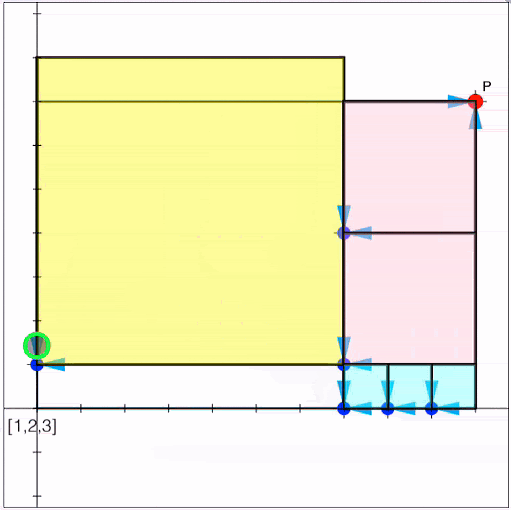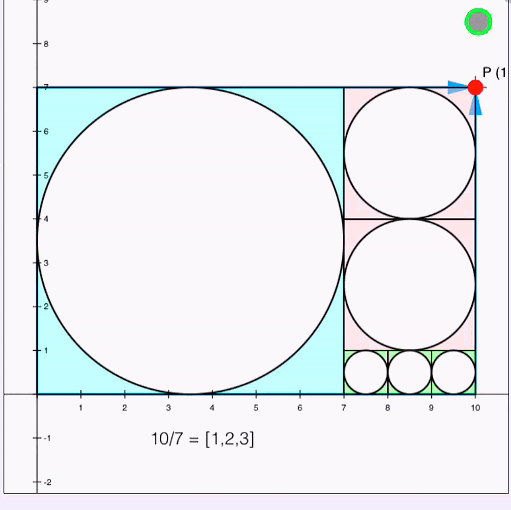
\[ \frac{10}{7}\]\[= 1+\frac{3}{7}\]\[= 1 + \frac{1}{\frac{7}{3}}\]\[= 1 + \cfrac{1}{2 + \cfrac{1}{3}} \]
Unlike irrational decimals, however, even irrational continued fractions can be predictable and are an ideal way to calculate approximate values - as accurately as you like!
Continued fractions have many practical applications but one of the most important lies in their ability to offer VERY good approximations to irrational numbers - the more convergents, the better the approximation. Indeed, each convergent gives the Best Approximation of the First Kind (look that up!) AND if a large value turns up in the list, then cutting the continued fraction just before that large value gives an extremely accurate approximation!
Study the examples which follow and see what you notice.
Some Examples
The Golden Ratio (or Golden Mean) (1 + sqrt(5))/2: \({1 + \sqrt 5} \over 2 \)
\[ \phi \approx 1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{1 + \cdots}}}} \]
Tap above or enter \phi in the MathBox below and press the f(x) button), OR for another approach, think of this continued fraction as \[x=1 + \cfrac{1}{x} => x^2=x+1\]
EXPLORE: Can you see why \(1+\sqrt{2} = (\frac{2+\sqrt{8}}{2})\) is called the silver mean and \(\frac{3+\sqrt{13}}{2}\) is the bronze mean? What would be their quadratic equations? Any suggestions for copper, nickel, aluminium or other metallic means?
Sqrt(2) ⇒ \[ \sqrt 2 \approx 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cdots}}}} \]
Tap above or enter \sqrt(2) in the MathBox below and press the f(x) button) - or try \[x=1 + \cfrac{1}{1+x} => x^2=2\]
EXPLORE: Can you find the quadratic equation form for \(\sqrt(3)\) or \(\sqrt(5)\)?
Pi ⇒ \[ \pi \approx 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292 + \cdots}}}} \]
(Tap above or enter \pi in the MathBox below and press the f(x) button) (but no closed form equation for this one!)
Continued fractions do come in more than one flavour.
In most cases, we deal with SIMPLE continued fractions, for which the numerators are all equal to 1, as shown above.
The famous Indian mathematician, Srinivasa Ramanujan, along with Euler, Gauss and other greats over many years have been fond of far more interesting varieties - visit GXWeb Fractured Functions to learn more about these amazing creatures.
\[ \pi \approx \cfrac{4}{1 + \cfrac{1^2}{3 + \cfrac{2^2}{5 + \cfrac{3^2}{7 + \cfrac{4^2}{9 + \cfrac{5^2}{11 + \cfrac{6^2}{13 + \cdots}}}}}}} \]
\[ e \approx 3 - \cfrac{1}{4 - \cfrac{2}{5 - \cfrac{3}{6 - \cfrac{4}{7 - \cfrac{5}{8 - \cfrac{6}{9+ \cdots}}}}}} \]
Continued fractions continue to be a source of research in many branches of mathematics. Use the tools available here to explore these wonderful mathematical opportunities!
You might notice that while simple continued fractions give predictable values for only a limited range of real numbers (the so-called Quadratic Irrationals), examples like these show that even the most transcendental of numbers can be expressed in predictable form. Observe, below, that continued fractions can also be expressed as the product of matrices!
Mathematics has been described as a search for patterns and relationships. What patterns and relationships did you find in these few examples? Use the tools which follow to explore your ideas further, and take a few moments to answer the questions that follow.
Once you have finished the questions, feel free to come back and continue to play with and learn more about these extraordinary numbers. They can be a gateway to interesting and important topics in mathematics, nature and computing.
Explore the Magic Table
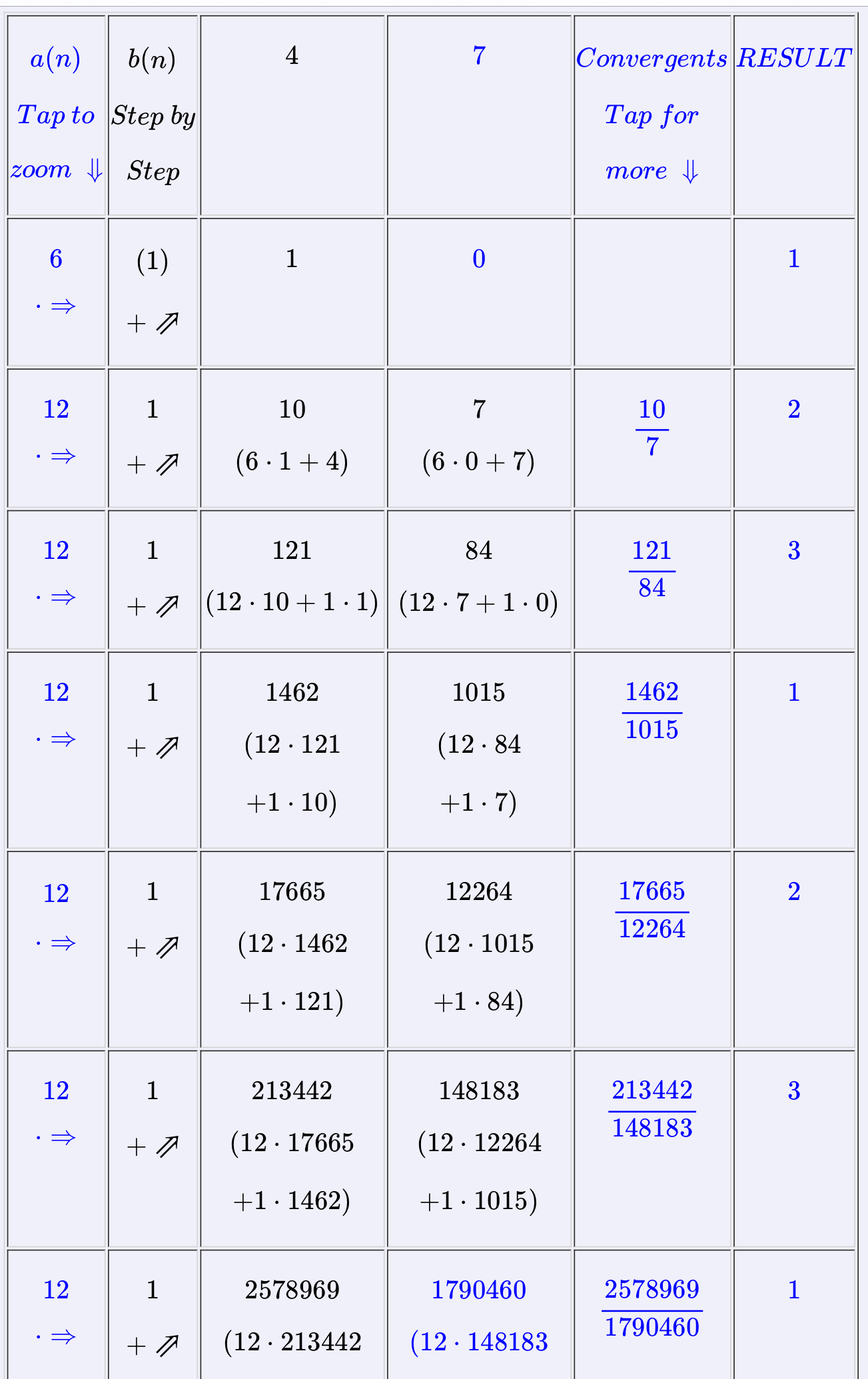
The magic table 1, 2 (first described by Gosper (1972) - credit for the name goes to Associate Professor Terry Gagen of the University of Sydney) offers a quick and simple way to generate the convergents of a continued fraction - it can even be used on linear fractional transformations of continued fractions.
For example, the continued fraction of
\[\sqrt(37) => \]\[a(n) = [6,12,12,12,12,12,12,...]\]\[b(n) = [1,1,1,1,1,1,1...]\] \[6 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12... }}}}}}}\] It is a simple matter to calculate a result such as
\[\begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \cdot \sqrt(37) \]where the linear fractional transformation is the matrix
\[\begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \ and \ \begin{bmatrix} 1 && 0 \\ 0 && 1 \end{bmatrix}\]represents the identity matrix.
Gosper's version of the magic table was presented horizontally, reading from right to left. A simplified form (which delivers each convergent in turn) might be represented as follows.
\[...\] \[12\] \[12\] \[12\] \[12\] \[12\] \[6\] \[...\] \[213442\] \[17665\] \[1462\] \[121\] \[10\] \[1\] \[4\] \[...\] \[148183\] \[12264\] \[1015\] \[84\] \[7\] \[0\] \[7\] Note that Gosper dealt only with simple continued fractions for which all b(n) (numerator) terms may be assumed to be 1.
For ease of presentation, in our version, the terms are displayed vertically, with the terms of the linear fractional transformation found at the top of the numerator and denominator columns (rotated -90°).
Tap to view:
Simple Convergent Form 1
Simple Convergent Form 2
Gosper Magic Table 1
Gosper Magic Table 2
Gosper Magic Table 3
Gosper Magic Table 4
Gosper Magic Table 5
In its simplest form, Gosper's Magic Table initially offers a convenient way to generate the convergents for a given continued fraction, along with a linear fractional transformation, expressed as a 2x2 matrix.
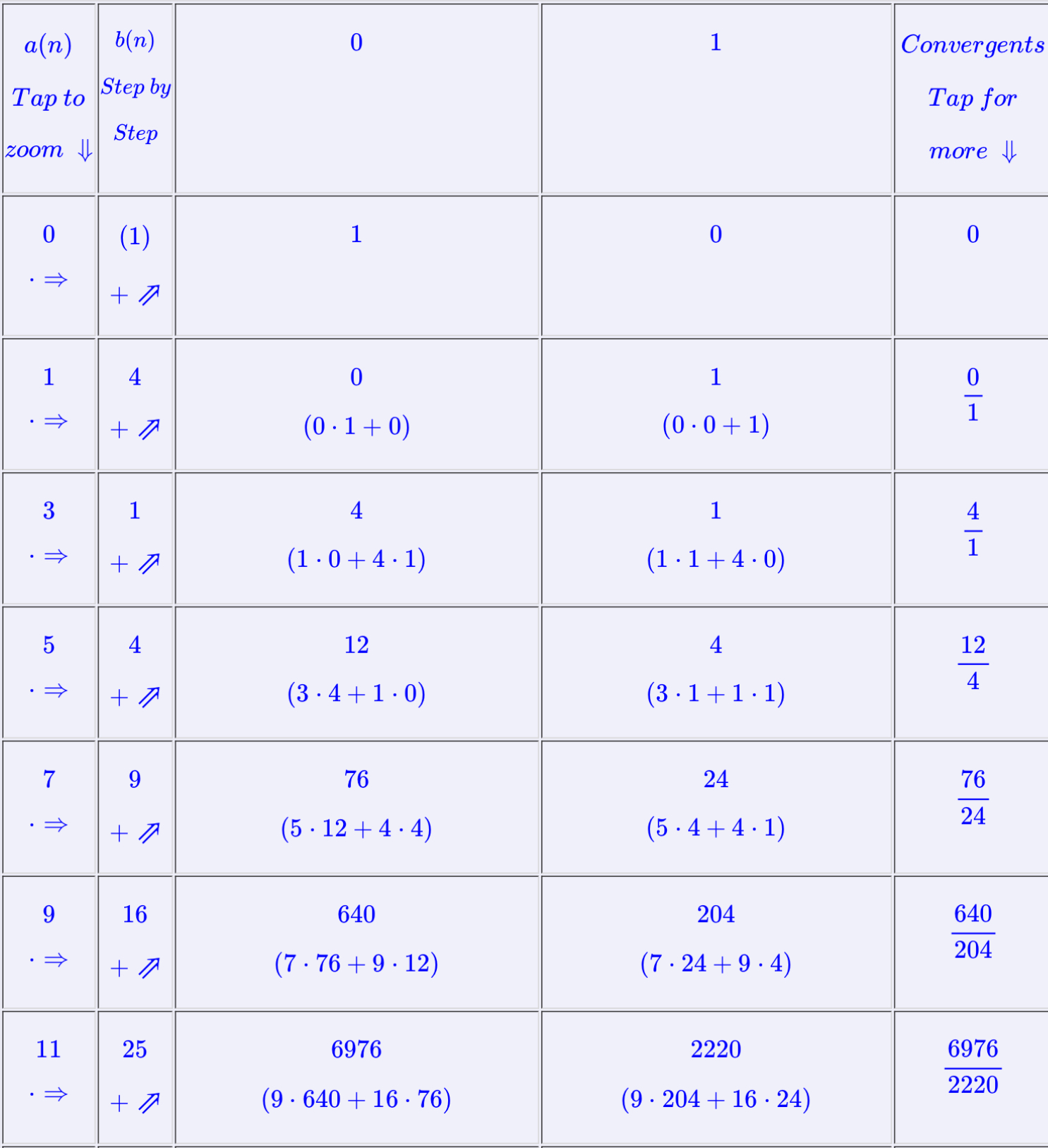
(Tap for an example) ⇑Note that the Magic Table presented here represents an extension of Gosper's method, supporting general continued fractions in addition to simple ones. For example, did you know that
\[\pi \approx 0 + \cfrac{4}{1 + \cfrac{1}{3 + \cfrac{4}{5 + \cfrac{9}{7 + \cfrac{16}{9 + \cfrac{25}{11 + \cfrac{36}{13 + \cfrac{49}{15 + \cfrac{64}{17 + \cfrac{81}{19...}}}}}}}}}}\]\[a(n) = [0,1,3,5,7,9,11,13,15,17,19]\]\[b(n) = [4,1,4,9,16,25,36,49,64,81]\]
Simple (Convergent)
Magic TableGosper
Magic TableEnter mtable(), or
mtable(sqrt(37)), or
mtable(sqrt(37),[1,4,0,7]), or even
mtable(sqrt(37),[1,4,0,7],0,12)Try one of Gosper's examples:
mtable(sqrt(2),[0,2,-1,3],0,12)Enter gmt(), or
gmt(sqrt(37)), or
gmt(sqrt(37),[1,4,0,7]), or even
gmt(sqrt(37),[1,4,0,7],0,12)Try one of Gosper's examples:
gmt(sqrt(2),[0,2,-1,3],0,12)You can also enter arrays: mtable([1,2,3,4,5],[1,0,0,1],0,12) or
mtable([[1,2,3,4],[4,3,2,1],[1,0,0,1],0,12)Try mtable([[2,1,2,3,4,5,6,7,8,9,10],[1,1,2,3,4,5,6,7,8,9,10],[1,0,0,1],0,12) or
mtable([[0,1,3,5,7,9,11,13,15,17,19],[4,1,4,9,16,25,36,49,64,81,100],[1,0,0,1],0,12).
Build Your Own Continued Fraction
To convert a real number (n) to a continued fraction is easy!
Try this yourself?
Step 1: Take the integer part of the number - floor[n] or Math.floor(n): This is your first index (call it \(a_0 \)), and first convergent.
Step 2: Subtract the integer part to leave the decimal part - the tail. \( Tail = n - floor(n) \)
Step 3: Calculate the reciprocal of the tail (\( 1 \over Tail \)) - this should give a number greater than or equal to 1.
Step 4: Take the integer part of this reciprocal value (\(a_1 = floor({ 1 \over Tail }) \)): This is your next index - call it \(a_1 \), and \({a_0 + {1 \over a_1}} \) the next convergent.
Step 5: Return to Step 2 and repeat the process...
But what if you want to go in the other direction? If you have a continued fraction, and would like to know the real number that it represents?
For rational numbers, this is easy, since the continued fraction is finite.
The most commonly used method involves starting from the bottom and working upwards.
Alternatively, try the Magic Table!
For most irrationals, finding the real number represented by a continued fraction is much harder, but not for quadratic irrationals, which are periodic.
Study the examples above for the golden ratio and the square root of 2. For any periodic continued fraction, we need to isolate the periodic part and use this to form a quadratic equation. For example...
\[ [1,2,3,1,2,3,1,2,3...] = 1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{3+...}}}}}\] \[ x = 1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{x}}}\]
Mathematical Toolkit
About the MathBoxes...
Hint: When entering mathematical expressions in the math boxes below (f(x), g(x) and h(x)), use the space key to step out of fractions, powers, etc. On Android, begin entry by pressing Enter.
Type simple mathematical expressions and equations as you would normally enter these: for example, "x^2[space]-4x+3", and "2/3[space]". For more interesting elements, use Latex notation (prefix commands such as "sqrt" and "nthroot3" with a backslash (\)): for example: "\sqrt(2)[space][space]". Learn More?
\[f(x)\]
\[g(x)\]
\[h(x)\]
\(a = \) -1 5 0 \(b = \) -1 5 0 \(c = \) -1 5 0 \\(d\\) -1 0 5 \\(e\\) -1 0 5 When entering mathematical expressions in the math boxes above (\(f\), \(g\) and \(h\)), use the space key to step out of fractions, powers, etc. On Android, begin entry by pressing Enter.
Type simple mathematical expressions and equations as you would normally enter these: for example, "x^2[space]-4x+3", and "2/3[space]". For more interesting elements, use Latex notation (prefix commands such as "sqrt" and "nthroot3" with a backslash (\)): for example: "\sqrt(2)[space][space]". More?
Continued Fraction Spreadsheet Explorer
This browser-based spreadsheet uses the handsontable JavaScript library.
WolframAlpha: CAS+
Sometimes, to deal with those stubborn, hard to reach problems, you need something stronger!
The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!
GeoGebra
GeoGebra offers another fast and accurate CAS alternative. You may also like to explore the GeoGebra web app.
Timing: Key Signature:
Share with QR Code
QR Codes are a great way to share data and information with others, even when no Internet connection is available. Most modern devices either come equipped with QR readers in-built, or freely available.
The default link here is the GXWeb Jigsaws and Quizzes, but you can use it as an alternative to sending your assessment data via email, web or share with others in your class. You can even use it to send your own messages!
GXWeb Jigsaws and Quizzes
Share Your Results
Enter your name:
My class:
Email to:
Session report length: 0 characters.
Turtle Robot Controls
Imagine designing, building and even remotely controlling your own robot! It is probably easier than you might think!
Alternatively, grab a TI Innovator Robot already made and follow the directions to "hack the hub"!
Watch the YouTube video of our GX Robot.
Follow the tutorial step-by-step directions to build and program your Arduino or TI Innovator robot.
NOTE: If using iPad or iPhone, you will need to grab the free Bluefy app to access webBluetooth since most browsers on this platform do not have this capability.
Then just connect and use your LOGO commands to steer - or use the controls below to connect and drive!
NOTE: Different surfaces and different robots will require different traction values. Try different values for distance and turn angle here until you find those that work best for your situation.
Distance Traction
Turn Traction
Manual Robot Controls
More to Explore: the Continued Fractions Collection
Interested to learn more? Delve more deeply into Continued Fractions with GXWeb Fractured Fractions and then on to the following...
Golden Numbers and More
Try \(\frac{34}{21}\), \(\frac{55}{34}\) and \(\frac{89}{55}\). Notice anything? What comes next?
This might just begin a search for the most beautiful (and most irrational) of numbers...! And make sure you take a moment to explore the archimidean spiral along the way:
Perhaps take another moment or two to also explore the metallic means: \[x=a + \cfrac{1}{x} => x^2=a\cdot x+1 => \frac{(a+\sqrt(4+a^2)}{2}\] and the noble numbers: \[x=a + \cfrac{1}{1-a+x} => (2\cdot (x-a)+1)^2 = 5 => \frac{(\sqrt(5)+2a-1)}{2}\].
Negative (or Reversal) Continued Fractions
Before considering general continued fractions, a note about the continued fractions of negative numbers.
\[\frac{10}{7} = [1,2,3] = 1+\cfrac{1}{2+\cfrac{1}{3}}\]Begin by observing that
\[-\frac{10}{7} \neq -1-\cfrac{1}{-2-\cfrac{1}{-3}} (= -\frac{2}{5})\]AND
\[-\frac{10}{7} \neq 1-\cfrac{1}{2-\cfrac{1}{3}} (= \frac{2}{5})\]However
\[-\frac{10}{7} = [-1,-2,-3] = -1+\cfrac{1}{-2+\cfrac{1}{-3}}\]and (perhaps surprisingly?)
\[\frac{10}{7} = [2,2,4]^- = 2-\cfrac{1}{2-\cfrac{1}{4}}\]
Did you know that there are TWO classical forms for continued fractions? I only found this out recently.
The simple or general form is built by taking the floor (or whole number part) of the fraction at each level and adding the reciprocal of the tail.
To convert a real number (n) to a continued fraction is easy!
The reversal or negative form takes instead the ceiling or next whole number value above, and subtracts the value of the term to form the tail! The reciprocal of this tail then forms the next term in the process.
To convert a real number (n) to a negative or reversal continued fraction is just as easy!
Try this yourself?
Step 1: Take the integer part of the number - floor[n] or Math.floor(n): This is your first index (call it \(a_0 \)), and first convergent.
Step 2: Subtract the integer part to leave the decimal part - the tail. \( Tail = n - floor(n) \)
Step 3: Calculate the reciprocal of the tail (\( 1 \over Tail \)) - this should give a number greater than or equal to 1.
Step 4: Take the integer part of this reciprocal value (\(a_1 = floor({ 1 \over Tail }) \)): This is your next index - call it \(a_1 \), and \({a_0 + {1 \over a_1}} \) the next convergent.
Step 5: Return to Step 2 and repeat the process...
Try this yourself?
Step 1: Round up to the integer above the number - ceil[n] or Math.ceil(n): This is your first index (call it \(a_0 \)), and first convergent.
Step 2: Subtract the current value from the integer part to leave the decimal part - the tail. \( Tail = ceil(n) - n \)
Step 3: Calculate the reciprocal of the tail (\( 1 \over Tail \)) - this should give a number greater than or equal to 1.
Step 4: Take the ceiling of this reciprocal value (\(a_1 = ceil({ 1 \over Tail }) \)): This is your next index - call it \(a_1 \), and \({a_0 + {1 \over a_1}} \) the next convergent.
Step 5: Return to Step 2 and repeat the process...
\[\frac{10}{7} = [1,2,2,1] \]\[= 1 + \cfrac{1}{2 + \cfrac{1}{2+\cfrac{1}{1}}}\] (Enter 10/7 or 1,2,3 or 1,2,2,1)
\[[\frac{10}{7}]^{-} = [2,2,4]^{-} \]\[= 2 - \cfrac{1}{2 - \cfrac{1}{4}}\] (Enter [10/7]^- or [2,2,4]^-
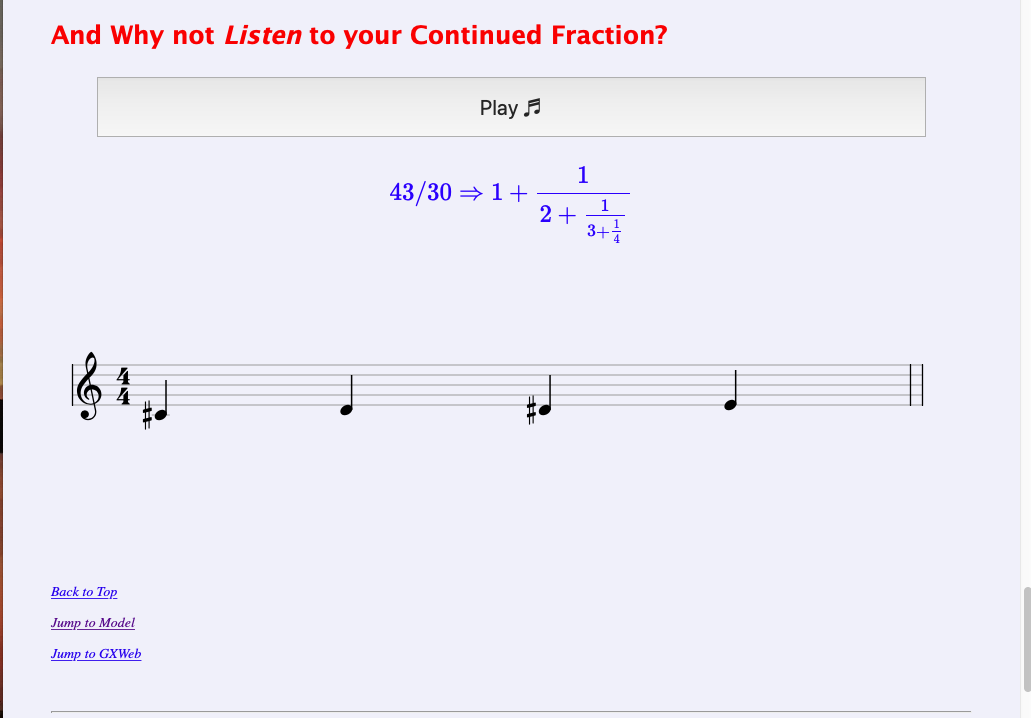
or [10/7]{neg} or [2,2,4]{neg})\[\frac{43}{30} = [1,2,3,4] \]\[= 1 + \cfrac{1}{2 + \cfrac{1}{3+\cfrac{1}{4}}}\] (Enter 43/30 or 1,2,3,4)
\[[\frac{43}{30}]^{-} = [2,2,5,2,2,2]^{-} \]\[= 2 - \cfrac{1}{2 - \cfrac{1}{5-\cfrac{1}{2-\cfrac{1}{2-\cfrac{1}{2}}}}}\] (Enter [43/30]^- or [2,2,5,2,2,2]^-
or [43/30]{neg} or [2,2,5,2,2,2]{neg})Try a few more examples and see if you can see a pattern...
HINT: It helps if your simple continued fraction form has an EVEN number of terms!
Converting to the Negative Form
With thanks to Morier-Genoud and Ovsienko (2019)
Let \(r\) and \(s\) be two coprime positive integers, and assume that \(r > s\). The rational number \(\frac{r}{s}\) has unique expansions
\[\frac{r}{s} = a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3+\cfrac{1}{...a_{2m}}}}\] \[= c_1 - \cfrac{1}{c_2 - \cfrac{1}{c_3-\cfrac{1}{...c_k}}}\]where \(a_i \geq 1\) and \(c_i \geq 2\) for all \(i\). The first is called a simple continued fraction and the second, a negative or reversal continued fraction.
Note that we can always assume a simple continued fraction has an even number of terms since every such continued fraction can be expressed in both a compact form (with last term not equal to 1) and an expanded form:
\[[a_1, a_2,..., a_n] = [a_1, a_2,..., a_{n-1}, 1]\]Then the terms of a negative or reversal continued fraction may be derived from those of the equivalent simple form as follows:
\[[c_1, c_2, c_3,..., c_{k-1}, c_k] = \] \[[a_1+1, 2 \ (repeated \ a_2-1\ times)..., \]\[a_3+1, 2 \ (repeated \ a_4-1\ times)..., \]\[a_{2m-1}+1, 2 \ (repeated\ a_{2m} \ times)]\]
Negative Terms in a Continued Fraction
As noted by Knott, LaGrange points out that it is a simple matter of algebra to show that we can remove subtractions in favour of addtions.
Wherever there is a subtraction, "push" it into the rest of the CF making positive numbers into negatives. We use C to represent the rest of a CF which may be empty or consist of one or more terms:
\[a - \frac{1}{b+C} = a + \frac{-1}{b+C} = a + \frac{1}{-b-C}\]Then if
\[C = \frac{1}{c+\frac{1}{d + \frac{1}{e+...}}}\]note that a negative value in a numerator ONLY changes the signs of the subsequent pair of numerator and denominator - this then flows on through the remaining terms to deliver an equal result without requiring any further sign changes.
\[a - \frac{1}{b+\frac{1}{c+\frac{1}{d + \frac{1}{e+...}}}}\] \[ = a + \frac{-1}{b+\frac{1}{c+\frac{1}{d + \frac{1}{e+...}}}}\] \[ = a + \frac{1}{-b-\frac{1}{c+\frac{1}{d + \frac{1}{e+...}}}}\] \[= a + \frac{1}{-b-\frac{1}{c+\frac{1}{d + \frac{1}{e+...}}}}\]Observe from the linked example that this holds for any occurrence within the terms of the continued fraction.
And for a pair of consecutive negative numerators?
\[a + \frac{1}{b-\frac{1}{c-\frac{1}{d + \frac{1}{e+...}}}}\] \[ = a + \frac{1}{b+\frac{-1}{c+\frac{-1}{d + \frac{1}{e+...}}}}\] \[= a + \frac{1}{b+\frac{1}{-c+\frac{1}{d + \frac{1}{e+...}}}}\]Simpler still!
Each consecutive pair of negative numerator values results in just a single negative leading term (denominator) in the second level. All other negative values cancel.
A string of sequential negative numerators, then, will result in alternating positive and negative leading terms.
Inverted Continued Fractions: Another Alternate Form?
Simple continued fractions are calculated by repeatedly taking the floor of a real number and inverting the remainder, resulting in a string of unit values as the numerators.
An alternative approach might involve setting all denominators (after the initial floor value) to 1.
\[\frac{24}{7} = 3 + \cfrac{1}{1 + \cfrac{2}{1+ \cfrac{1}{1+ \cfrac{2}{1+ \cfrac{1}{1}}}}}\]\[[3,1,1,1,1,1]\]\[[1,2,1,2,1,1]\]\[\approx 3.4285714285714284\]\[⇒ \ Convergents:\]\[[3,4,\frac{10}{3},\frac{7}{2}, \frac{17}{5}, \frac{24}{7}]\]\[Error = 0 \%\]But how might this be achieved?
And would such an approach offer any practical benefits?
Try the inverted continued fraction for Eulers Number \(e\).
Certain surds such as \(\sqrt(2)\), \(\sqrt(5)\) and \(\sqrt(10)\) (square roots of the form \(n^2+1\)?) are also of interest.
Explore...
\[\frac{24}{7} = 3 + \frac{3}{7}\]\[= 3 + \cfrac{1}{\frac{7}{3}}\]\[= 3 + \cfrac{1}{1 + \frac{4}{3}}\]\[= 3 + \cfrac{1}{1 + \cfrac{2}{2 \cdot \frac{3}{4}}}\cdots \]\[where \ 2 = \lceil \frac{4}{3}\rceil \ and \ \frac{2}{2 \cdot \frac{3}{4}} = \frac{4}{3} \]\[Then \ 2\cdot \frac{3}{4} - 1 = \frac{3}{2} - 1 = \frac{1}{2}\]\[= 3 + \cfrac{1}{1 + \cfrac{2}{1 + \cfrac{1}{1 + \frac{1}{1/2} \cdots }}}\] \[Initially, \ let \ a = \lfloor x \rfloor, \ b = x - a \]\[⇒ \ x = a + b\]\[Let \ c = \lceil b\rceil \ ( = 1) \ and \ b = \frac{1}{b} \]\[ ⇒ x = a + \cfrac{c}{c\cdot b} = a + \cfrac{1}{b}\]\[Subsequent \ steps: \]\[ Let \ a = 1, \ b = \frac{c}{b}-a\]\[⇒ x = a + \cfrac{1}{1 + b}\]\[Then \ let \ c = \lceil b \rceil \ and \ b = \frac{c}{c\cdot (\frac{1}{b})}\]\[x = a + \cfrac{1}{1 + \frac{c}{c\cdot (\frac{1}{b}) \cdots }} \]
Fractured Functions: Generalised Continued Fractions
Most of the continued fractions you will come across are likely to be of the simple variety, but the many generalised forms offer so many interesting patterns and possibilities for further exploration! Try a few and see what you discover...
Simple Quadratic Continued Fractions
More Quadratic Continued Fractions
Euler's Numbers (\(e^x\))
Euler's Numbers (\(log(1+\frac{x}{y})\))
Pieces of Pi
Not So AbSurd After All
Continued Fractions Arithmetic
Continued Logarithms
\[ x^2 = m\]
\[ x^2 = a^2 + b\]
\[ x^2 - a^2 = b\]
\[ (x-a)(x+a) = b\]
\[ x -a = \frac{b}{a+x}\]
\[ x = a + \frac{b}{a+x}\]
Some Matrix Fraction Magic
As seen already, continued fractions can be represented in matrix form, offering some interesting possibilities - and applicable to both simple and generalised continued fractions.
1. Continued Fraction Matrices
The most-commonly documented approach involves the product of 2 x 2 matrices.
\[a_0+\cfrac{b_0}{a_1 + \cfrac{b_1}{a_2 + \cfrac{b_2}{a_3 + \cfrac{b_3}{a_4...}}}} = \]\[\begin{bmatrix} a_0 & b_0 \\ 1 & 0 \end{bmatrix}\cdot \begin{bmatrix} a_1 & b_1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_2 & b_2 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_3 & b_3 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_4 & 1 \\ 1 & 0 \end{bmatrix}... \]
For example, arithmetic operations can be readily expressed.
\[ [1,2,3,1,2,3,1,2,3,1...] =>\]\[1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1...}}}}}}\]\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\cdot \begin{bmatrix} 2 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} ...\] \[ x = 1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{x}}} \]\[= \frac{4+\sqrt(37)}{7} \] \[If... \sqrt{37}= 6+ \cfrac{1}{12+\cfrac{1}{12+\cfrac{1}{12+\cfrac{1}{12+...}}}}\]\[=> \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} ... \] \[Then... \frac{4+\sqrt(37)}{7} = \begin{bmatrix} 1 & 4 \\ 0 & 7 \\ \end{bmatrix} \cdot \sqrt{37} \]\[ => \begin{bmatrix} 1 & 4 \\ 0 & 7 \\ \end{bmatrix} \cdot \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 12 & 1 \\ 1 & 0 \\ \end{bmatrix} ... \]Even less predictable ones:
\[ [2,2,3,1,1,2,3,1,1,2,3...] =>\]\[2 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{3...}}}}}}\] \[ \begin{bmatrix} 2 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} ... \] \[ x-1 = 1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{1}{1 + \cfrac{1}{x-1}}}} \]\[ x-1 = 1 + \cfrac{1}{2 + \cfrac{1}{3 + \cfrac{x-1}{x}}} \]\[= \frac{4+\sqrt(11)}{3} \] \[If...\sqrt{11}= 3+ \cfrac{1}{3+\cfrac{1}{6+\cfrac{1}{3+\cfrac{1}{6+...}}}}\]\[=> \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} ... \] \[Then... \frac{4+\sqrt(11)}{3} = \begin{bmatrix} 1 & 4 \\ 0 & 3 \\ \end{bmatrix} \cdot \sqrt{11} \]\[ => \begin{bmatrix} 1 & 4 \\ 0 & 3 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 6 & 1 \\ 1 & 0 \\ \end{bmatrix} ... \]
2. Tridiagonal Matrix Continued Fractions
Two alternative approaches involve larger square (tridiagonal) matrices. (eg Frommer, Kahl and Tsolakis (2021) and Qi, Wen Guo and Lim (2020))
\[Let \ M = \begin{bmatrix} a_0 & b_0 & 0 & 0 & 0 \\ -1 & a_1 & b_1 & 0 & 0 \\ 0 & -1 & a_2 & b_2 & 0 \\ 0 & 0 & -1 & a_3 & b_3 \\ 0 & 0 & 0 & -1 & a_4\end{bmatrix}\]Then taking the inverse of M, the first ([1,1]) term gives the reciprocal of the final convergent of the continued fraction:
\[\frac{1}{inv(M)[1,1]} = a_0+\cfrac{b_0}{a_1 + \cfrac{b_1}{a_2 + \cfrac{b_2}{a_3 + \cfrac{b_3}{a_4}}}}\]A second approach involves the determinants of two square matrices, p and q as follows:
\[a_0+\cfrac{b_0}{a_1 + \cfrac{b_1}{a_2 + \cfrac{b_2}{a_3 + \cfrac{b_3}{a_4}}}} = \frac{det(p)}{det(q)}\]
Some expected relationships...
And even some unexpected ones!
Tap on the matrix examples above and follow the directions. Then just press \(h\) (at the end, you may need to press the TextBoxes button to lay out the result correctly).
3. Matrix as Mediant: Building the Stern-Brocot Tree
Returning to 2 x 2 matrices, we find another surprisingly simple and powerful matrix approach to building the Stern-Brocot Tree (van der Poorten and Wildberger), and consequently, listing all possible rationals.
We begin by viewing 2 x 2 matrices in a new way, defining the mediant:
\[\begin{bmatrix} a & b \\ c & d \end{bmatrix} => \frac{a}{c} ⊕ \frac{b}{d} = \frac{a+b}{c+d}\]Then the familiar identity matrix becomes
\[\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} =>\frac{1}{0} ⊕ \frac{0}{1} = \frac{1+0}{0+1} = \frac{1}{1}\]Now we define two matrices, which will serve as left (L) and right (R) steps for our tree:
\[L = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \ and \ R = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\]Then any term of our Stern-Brocot Tree can be represented by a matrix
\[M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]with parents \(\frac{a}{c}\) and \(\frac{b}{d}\) and determinant 1. Such a matrix can serve as the parent for two further matrices:
\[M \cdot L = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \ and \ M \cdot R = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\] \[M\cdot L = \begin{bmatrix} a+b & b \\ c+d & d \end{bmatrix} \ and \ M\cdot R = \begin{bmatrix} a & a+b \\ c & c+d \end{bmatrix}\] \[M\cdot L => \frac{a+2\cdot b}{c+2\cdot d} \ and \ M\cdot R => \frac{2\cdot a+ b}{2\cdot c+ d}\]
Beginning with our identity matrix
\[M = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} => \frac{1+0}{0+1} = \frac{1}{1}\]Notice the parents of \(\frac{1}{1}\) are \(\frac{0}{1}\) and \(\frac{1}{0}\)?
We quickly see the effects of a Left and Right step:
\[M \cdot L = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \ and \ M \cdot R = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\] \[M\cdot L = \begin{bmatrix} 1+0 & 0+0 \\ 0+1 & 0+1 \end{bmatrix} \ and \ M\cdot R = \begin{bmatrix} 1+0 & 1+0 \\ 0+0 & 0+1 \end{bmatrix}\] \[M\cdot L = \begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \ and \ M\cdot R = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} *\] \[M\cdot L => \frac{1+0}{1+1} \ and \ M\cdot R => \frac{1+ 1}{0+ 1}\] \[M\cdot L => \frac{1}{2} \ and \ M\cdot R => \frac{2}{1}\]Line * shows that the parents of \(\frac{1}{2}\) are \(\frac{0}{1}\) and \(\frac{1}{1}\) and the parents of \(\frac{2}{1}\) are \(\frac{1}{1}\) and \(\frac{1}{0}\)?
Refer back to the section Building the Fraction Trees to see this process in more detail, and try some for yourself!
See a live demo?
Play more with continued fractions?
Continued Fraction Arithmetic
Contrary to everybody, this self contained paper will show that continued fractions are not only perfectly amenable to arithmetic, they are amenable to perfect arithmetic. (Bill Gosper, 1972)
For Gosper, the appealing concept of perfect arithmetic may well have involved using continued fractions to perform calculations to any desired degree of accuracy. Continued fractions are ideal tools for successive approximation.
The examples explored here may offer a glimpse into one of the enduring questions regarding continued fractions: they are wonderful at representing numbers, both rational and irrational, but can they also serve as practical tools for computation?
While some of these examples involve simple, finite rational values, it is unlikely that anyone would realistically wheel in continued fraction arithmetic for such questions as \(\frac{10}{7} + \frac{22}{5}\).
But for those convoluted rationals and especially those infinite irrationals? Well... it was made for such as these!
Continued Logarithms
While continued fractions may formally trace their origins to the time of Euclid, continued (binary) logarithms owe their inception to Bill Gosper in his 1972 unpublished paper on continued fraction arithmetic.
In the newly dawning age of personal computers, Gosper recognised both the limitations of continued fractions in dealing with very large and very small numbers, and the possibilities for a new type of binary representation, reducing such numbers to highly accurate arrays of zeros and ones. Gosper described it as a "sort of recursive version of scientific notation" (1972).
This exploration introduces just a taste of the wonderful research of the past decade, exploring these unusual mathematical creatures. The particular focus here is on the multiple continued fraction-like representations for real numbers made explicit through continued logarithms.
While we count ourselves lucky to know of one or two generalized continued fraction forms for most reals, this exploration reveals the relatively simple processes which deliver five distinct forms for most numbers!
Simple Continued Fractions may be defined as follows:
\[f(x) = \left\{ \begin{array}{ll} (x-1) & x\geq 1 \\ \frac{1}{x} & 0\lt x\lt 1 \\ terminate & x=0 \\ \end{array} \right. \]
Count the number of times we encounter \[x ⇒ x − 1\] before we either reciprocate or terminate. These counts are the terms \[[a_0, a_1,...]\] of our continued fraction.
Continued Logarithms (base \(b\)) (Gosper, 1978) are defined in a similar way by
\[g(x) = \left\{ \begin{array}{ll} \frac{x}{b} & x\geq b \\ \frac{b-1}{x-1} & 1\lt x\lt b \\ terminate & x=1 \\ \end{array} \right. \]
For \(x \geq b\), divide by \(b\) until the result lies between 1 and \(b\). Count the number of divisions. Continue until you reach 1.
For \(1 < x < b\), subtract 1 from base \(b\) then divide by \((x-1)\). Repeat until the result is equal to 1 (and terminate) or greater than or equal to \(b\) (and start dividing by \(b\) again)..
The continued logarithm for \(19\)\[ => [1,1,1,1,0,1,1,0,1,0,1]_{cl(2)}\]\[ => [4,2,1,1]_{cl(2)}\]
\[19 = 2^4+\cfrac{2^4}{2^2+\cfrac{2^2}{2^1+\cfrac{2^1}{2^1}}}\] \[= 16+\cfrac{16}{4+\cfrac{4}{2+\cfrac{2}{2}}}\]
The continued logarithm for \(\frac{21}{5}\)\[=> [1,0,1,0,1]_{cl(3)}\]\[=> [1,1,1]_{cl(3)}\]
\[\frac{21}{5} = 3^1+\cfrac{2\cdot 3^1}{3^1+\cfrac{2\cdot 3^1}{3^1}}\] \[= 3+\cfrac{6}{3+\cfrac{6}{3}}\]
Continued Fractions and Farey Trees
Suppose you wanted to make a list of all the rational numbers between 0 and 1.
How might you start?
One approach might be to begin with the denominators of the fractions: first, list those with denominator 1 - zero and 1: \(\frac{0}{1}, \frac{1}{1} \).
Next, add those with denominator 2: \(\frac{0}{1}, \frac{1}{2}, \frac{1}{1} \).
Add those with denominator 3 ( \(\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1} \)) and you are on your way to the Farey Sequence! This last would be referred to as the Farey Sequence of Order 3.
There are some wonderful connections between continued fractions and Farey numbers - rational terms of Farey Sequences.
For example, \(\frac{2}{5}\) and \(\frac{5}{12}\) are neighbours in Farey(12), as are \( \frac{6}{19}\) and \(\frac{7}{22}\) in Farey(25). Check their continued fraction forms and try more of your own...
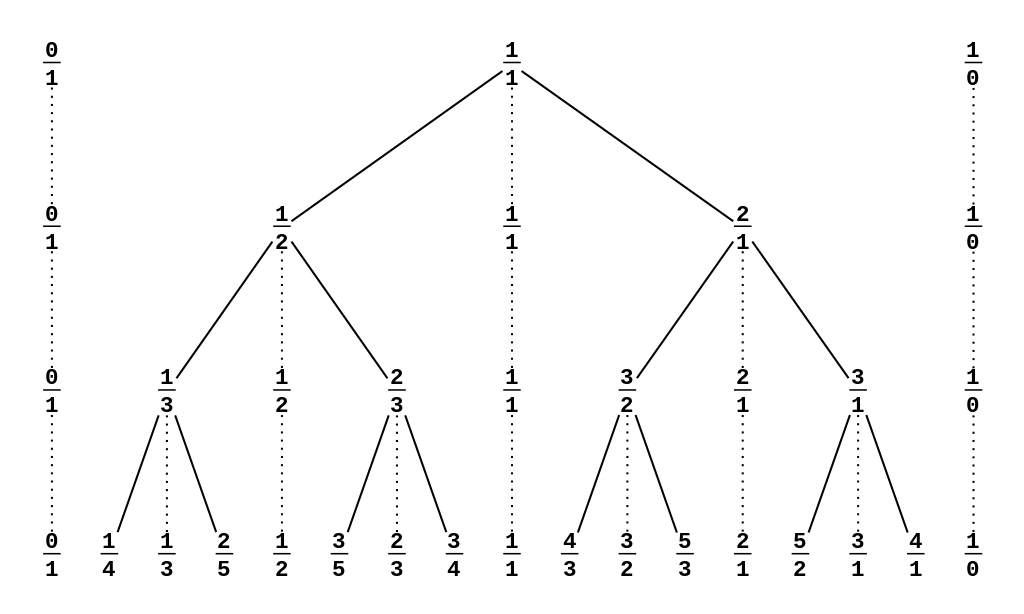
Climb Around the Farey (Stern-Brocot) Tree
In addition to the Farey Sequence, there are other beautiful ways to display the rationals between 0 and 1, including one which is even more closely related to continued fractions.
The Farey Tree (a subset of the Stern-Brocot Tree) begins with the endpoints of 0 and 1 and uses the mediant to find a fraction between each. As with the Farey sequence, this simply involves forming a fraction by adding the two numerators and the two denominators.
So \(\frac{0}{1}\) and \(\frac{1}{1}\) give \(\frac{0+1}{1+1} = \frac{1}{2}\)
Then \(\frac{0}{1}\) and \(\frac{1}{2}\) give \(\frac{0+1}{1+2} = \frac{1}{3}\) and \(\frac{1}{1}\) and \(\frac{1}{2}\) give \(\frac{1+1}{1+2} = \frac{2}{3}\)
\[\frac{0}{1}\] \[\frac{1}{1}\]
\[\frac{0+1}{1+1}\]\[\frac{1}{2}\]
\[\frac{0+1}{1+2}\]\[\frac{1}{3}\] \[\frac{1+1}{1+2}\]\[\frac{2}{3}\] Each subsequent row of fractions is built by continuing this process, stepping either to the left (L) or right (R), beginning from 1. Each \(n\)-th row begins with \(\frac{1}{n}\) and ends with \(\frac{n-1}{n}\).
From \(\frac{1}{1}\), to get to \(\frac{1}{2}\), move down to the Left (L). To form the continued fraction(s), simply add another L or R (it does not matter which because both deliver correct but slightly different results). So for \(\frac{1}{2}\), we could have LL or LR. Begin your continued fraction with zero (since all our fractions - for now! - lie between 0 and 1) and then count each repeated element. Then LL will give the continued fraction \([0, 2]=0+\cfrac{1}{2}\) and LR gives \([0, 1, 1] = 0 + \cfrac{1}{1+\cfrac{1}{1}}\).
In the same way, to get to \(\frac{1}{3}\) from \(\frac{1}{1}\), step LL. Add another L to get LLL (\([0,3]\)) or LLR (\([0,2,1]\)). For \(\frac{2}{3}\) from \(\frac{1}{1}\), step LR. Add another L to get LRL (\([0,1,1,1]\)) or LRR (\([0,1,2]\)).
Any continued fraction ending in 1 can be compacted by adding that trailing one to the previous term.
\[\frac{0}{1}\]\[[0]\] \[\frac{1}{1}\]\[[1]\]
\[\frac{1}{2}\]\[L+L\]\[[0,2]\]\[L+R\]\[[0,1,1]\]
\[\frac{1}{3}\]\[LL+L\]\[[0,3]\]\[LL+R\]\[[0,2,1]\] \[\frac{2}{3}\]\[LR+R\]\[[0,1,2]\]\[LR+L\]\[[0,1,1,1]\]
Follow a Binary Path to Continued Fractions
Finally, note that every element of our Farey Tree can be allocated its own unique number, starting with \(\frac{1}{2}\) as number 1, then stepping down and counting from right to left. This gives \(\frac{2}{3}\) as number 2, \(\frac{1}{3}\) in position 3 and \(\frac{3}{4}\) as the fourth Farey Tree fraction.
Now, suppose instead of L and R we used 1 to represent a step down and to the left and 0 to step down and to the right?
We saw above that the path to fraction number 1 (\(\frac{1}{2}\)) from the starting point of \(\frac{1}{1}\) is simply L to which we add another L to give LL (2) or R for LR (1,1). Now add a 0 at the front to form the equivalent continued fractions [0,2] and [0,1,1].
But instead of L to represent the path, we could use 1. Then add a trailing 1 (11 → 2), and a leading 0 and we have the continued fraction [0,2] (since we are counting repeated elements). If we had added a trailing zero, then after the leading 0 we have one "1" (or L) and one "0" (or R) and so we get [0,1,1], as required.
Now consider a different approach. Suppose I wish to know which fraction occurs in the 17th position of our tree.
In binary form, 17 = 10001 (1x16, 0x8, 0x4, 0x2, 1x1). This can also be expressed as the path LRRRL.
Adding a leading zero, and a trailing L leads to the continued fraction [0,1,3,2] (or [0,1,3,1,1] if we had added a trailing R). These both represent the fraction \(\frac{7}{9}\) which is indeed our 17th fraction!
Wait... what?
So I can find the continued fraction of any rational between 0 and 1 by expressing its position on the Farey Tree as a binary number, add a 0 or 1 at the end, count the repeated elements and stick a 0 at the front?
In fact, there is one final bonus. What if we don't add the zero at the front? Then instead of \(\frac{7}{9}\) we get \(\frac{9}{7}\) and suddenly we are no longer restricted to rationals between 0 and 1 but potentially any rational number could be expressed in this way!
We are now in the realm of the Stern-Brocot Tree, of which our Farey Tree is just one half!
Take some time to explore this amazing tree, then try the questions which follow.
\[\frac{0}{1}\]\[[0]\] \[\frac{1}{1}\]\[[1]\]
\[\frac{1}{2}\]\[L+L\]\[[0,2]\]\[L+R\]\[[0,1,1]\]\[(1)\]
\[\frac{1}{3}\]\[LL+L\]\[[0,3]\]\[LL+R\]\[[0,2,1]\]\[11\]\[(3)\] \[\frac{2}{3}\]\[LR+R\]\[[0,1,2]\]\[LR+L\]\[[0,1,1,1]\]\[10\]\[(2)\]
\[\frac{1}{4}\]\[LLL+\]\[[0,4]\]\[[0,3,1]\]\[111\]\[(7)\] \[\frac{2}{5}\]\[LLR+\]\[[0,2,2]\]\[[0,2,1,1]\]\[110\]\[(6)\] \[\frac{3}{5}\]\[LRL+\]\[[0,1,1,2]\]\[[0,1,1,1,1]\]\[101\]\[(5)\] \[\frac{3}{4}\]\[LRR+\]\[[0,1,3]\]\[[0,1,2,1]\]\[100\]\[(4)\]
\[\frac{1}{5}\] LLLL+L
[0,5]
1111
(15)
\[\frac{2}{7}\] LLLR+R
[0,3,2]
1110
(14)
\[\frac{3}{8}\] LLRL+L
[0,2,1,2]
1101
(13)
\[\frac{3}{7}\] LLRR+R
[0,2,3]
1100
(12)
\[\frac{4}{7}\] LRLL+L
[0,1,1,3]
1011
(11)
\[\frac{5}{8}\] LRLR+R
[0,1,1,1,2]
1010
(10)
\[\frac{5}{7}\] LRRL+L
[0,1,2,2]
1001
(9)
\[\frac{4}{5}\] LRRR+R
[0,1,4]
1000
(8)
\[\frac{1}{6}\] (31)
\[\frac{2}{9}\] (30)
\[\frac{3}{11}\] (29)
\[\frac{3}{10}\] (28)
\[\frac{4}{11}\] (27)
\[\frac{5}{13}\] (26)
\[\frac{5}{12}\] (25)
\[\frac{4}{9}\] (24)
\[\frac{5}{9}\] (23)
\[\frac{7}{12}\] (22)
\[\frac{8}{13}\] (21)
\[\frac{7}{11}\] (20)
\[\frac{7}{10}\] (19)
\[\frac{8}{11}\] (18)
\[\frac{7}{9}\] (17)
\[\frac{5}{6}\] (16)
Tap on any table cell above for more
Test Yourself
What fraction lies at the end of the path LLRR(+R) (or LLRR(+L))? (Tap for the answer)
What fraction has continued fraction [0, 1, 1, 1, 2] (or [0, 1, 1, 1, 1, 1])? (Tap for the answer)
What do you notice about the sums of each continued fraction on the same row? (Tap for the answer)
What do you notice about the numerators of the fractions across each row? (Tap for the answer)
What about the denominators of each fraction across each row? (Tap for the answer)
What fraction occupies position 40 on the Farey Tree? (Tap for the answer)
Explore the Stern-Brocot Tree
This expanded version of the Stern-Brocot Tree covers all rational numbers using symmetry and reciprocals!
You will find the Farey Tree as the left half of the mirror image making up this tree - rational numbers between 0 and 1 to the left; all other rationals on the right.
Try some Stern-Brocot values yourself!
The Stern-Brocot Tree has its own continued fraction! (thanks to Dr Bruce Bates from the University of Wollongong)
(Note that this is not the usual simple continued fraction with all numerators equal to 1. This is a general continued fraction - all but the leading numerator equal -1. For convenience, we will use the continued fraction list form below, but a stricter form might be [(0,1),(3,-1),(1,-1),(3,-1),(1,-1)].)
\[[0,3,1,3,1]\] The (Left Branch) Stern-Brocot Continued Fraction of order 3 is
(The Right Branch Stern-Brocot Continued Fraction of order 3 is \([3,1,3,1]\))
\[0+\cfrac{1}{3-\cfrac{1}{1-\cfrac{1}{3-\cfrac{1}{1}}}}\] Each convergent of the Stern-Brocot continued fraction gives a term in the Farey Sequence of order 3:
\[\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}\]Adding the terms from the right-branch Stern-Brocot continued fraction (above) OR just some reciprocal mirroring of the terms, we then get the full Stern-Brocot sequence of order 3:
\[\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1}, \frac{3}{2}, \frac{2}{1}, \frac{3}{1}\]Can you see how this may be expressed as a product of matrices?
\[\begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 3 & -1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & -1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 3 & -1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & -1 \\ 1 & 0 \\ \end{bmatrix}\] \[= \frac{1}{1}\]⇒ \[\begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 3 & -1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 3 & -1 \\ \end{bmatrix} => \frac{0}{-1}, \frac{1}{3}\] \[\begin{bmatrix} 1 & 0 \\ 3 & -1 \\ \end{bmatrix} \begin{bmatrix} 1 & -1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ 2 & -3 \\ \end{bmatrix} => \frac{1}{2}\] \[\begin{bmatrix} 1 & -1 \\ 2 & -3 \\ \end{bmatrix} \begin{bmatrix} 3 & -1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ 3 & -2 \\ \end{bmatrix} => \frac{2}{3}\] \[\begin{bmatrix} 2 & -1 \\ 3 & -2 \\ \end{bmatrix} \begin{bmatrix} 1 & -1 \\ 1 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & -2 \\ 1 & -3 \\ \end{bmatrix} => \frac{1}{1}\]
So where does this mysterious continued fraction come from?
Order (0) n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15... 2 (0) 2 1 3 (0) 3 1 3 1 4 (0) 4 1 3 1 5 1 3 1 5 (0) 5 1 3 1 5 1 3 1 7 1 3 1 5 1 3 1 Can you see a pattern?
Not an easy one at all...
Hint: The tree(s) we are building are binary. Each row increases by a multiple of two as each term on one row is the parent of two children.
Look again at our continued fraction arrays. The first two terms are easy: the leading zero of a continued fraction ensures that the value lies between 0 and 1. The second term is the order number.
Now study the remaining terms in the n-th sequence: all odd-numbered terms are given the value 1.
So what about the even numbers? 2 → 3 (\(2\cdot 1+1\))? 4 → 5 (\(2\cdot 2+1\))? But for 6, \(2\cdot 3+1\) does not equal 5, and for 8, \(2\cdot 4+1\) does not equal 7 as required.
The secret here lies in counting the number of 2s in the prime factorisation of each number!
Let b be the number of times 2 occurs as a factor of each number:
- \(2=2\cdot 1\) so b = 1 and \(2\cdot b + 1 = 3\).
- \(4=2\cdot 2\cdot 1\) so b = 2 and \(2\cdot b + 1 = 5\).
- \(6=2\cdot 3\) so b = 1 and \(2\cdot b +1 = 3\).
- \(8=2\cdot 2\cdot 2\cdot 1\) so b = 3 and \(2\cdot b +1 = 7\).
Order (0) n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15... n → b (0) n
↓
b20
↓
021
↓
120\(\cdot\)3
↓
022
↓
220\(\cdot\)5
↓
021\(\cdot\)3
↓
120\(\cdot\)7
↓
023
↓
320\(\cdot\)9
↓
021\(\cdot\)5
↓
120\(\cdot\)11
↓
022\(\cdot\)3
↓
120\(\cdot\)13
↓
021\(\cdot\)7
↓
120\(\cdot\)15
↓
0\(2\cdot b+1\) (0) n 1 3 1 5 1 3 1 7 1 3 1 5 1 3 1
As we see above, the Stern-Brocot Tree adds a symmetrical but reciprocal copy of the Farey Tree.
Where the terms of the Farey Tree all lie between 0 and 1, their reciprocals, of course, are all greater than 1.
In this way, the Stern-Brocot Tree offers a listing of ALL rationals.
Explore the Calkin-Wilf Tree
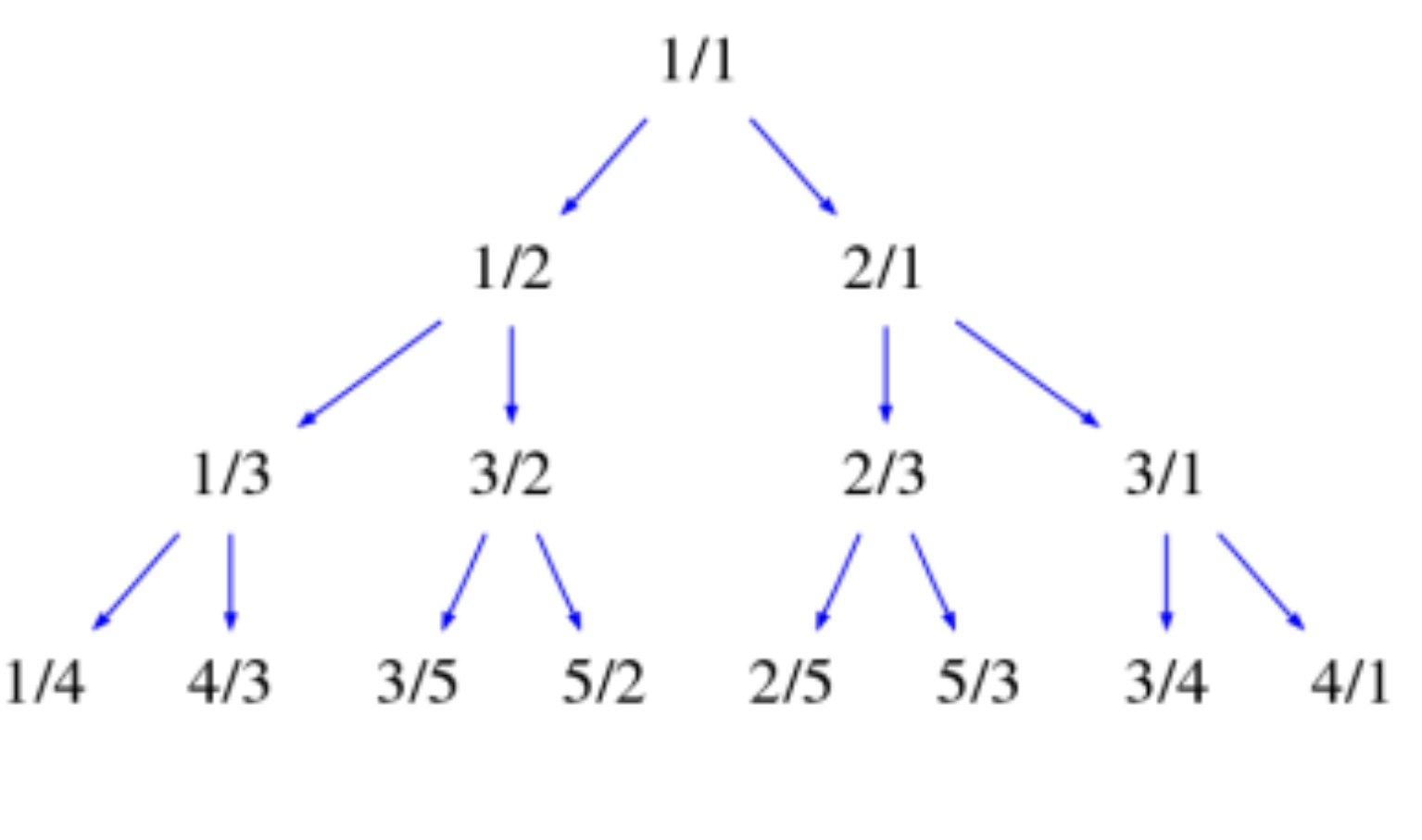
The Calkin-Wilf tree (or Tree of All Fractions) is another binary tree which is obtained by starting with the fraction 1/1 and (this time!) adding \(\frac{a}{a+b}\) and \(\frac{a+b}{b}\) iteratively below each fraction \(\frac{a}{b}\).

The Calkin-Wilf Tree was only developed in the year 2000 by Neil Calkin and Herb Wilf (demonstrating that there is still much beautiful and useful mathematics to be discovered), and is also similar to the binary tree of Johannes Kepler (1619) (The image ⇒ shows the Calkin-Wilf rule on the left and Kepler's on the right).
This tree (like the Stern-Brocot tree) generates every rational number. Writing out the terms in a sequence gives
\(\frac{1}{1}, \frac{1}{2}, \frac{2}{1}, \frac{1}{3}, \frac{3}{2}, \frac{2}{3}, \frac{3}{1}, \frac{1}{4}, \frac{4}{3}, \frac{3}{5}, \frac{5}{2}, \frac{2}{5}, \frac{5}{3}, \frac{3}{4}, \frac{4}{1}\)...
The sequence has the property that each denominator is the next numerator. That means that the nth rational number in the list looks like \(\frac{b(n)}{b(n + 1)}\) (n = 0, 1, 2, . . .), where
{b(n)}n≥0 = {1,1,2,1,3,2,3,1,4,3,5,2,5,3,4,1,5,4,7,...}.
This is a bit remarkable - at very least, for its efficiency. This single list can be viewed in (at least) three ways:
As the list of numerators of the Calkin-Wilf Tree,
As the list of denominators of the Calkin-Wilf Tree (after removing the first term) OR
As the actual list of fractions of the Calkin-Wilf Tree by taking each term with its next term!
Different from the Stern-Brocot tree above, the rationals between 0 and 1 are paired (interleaved) with their reciprocal complements.
Try some Calkin-Wilf values yourself!
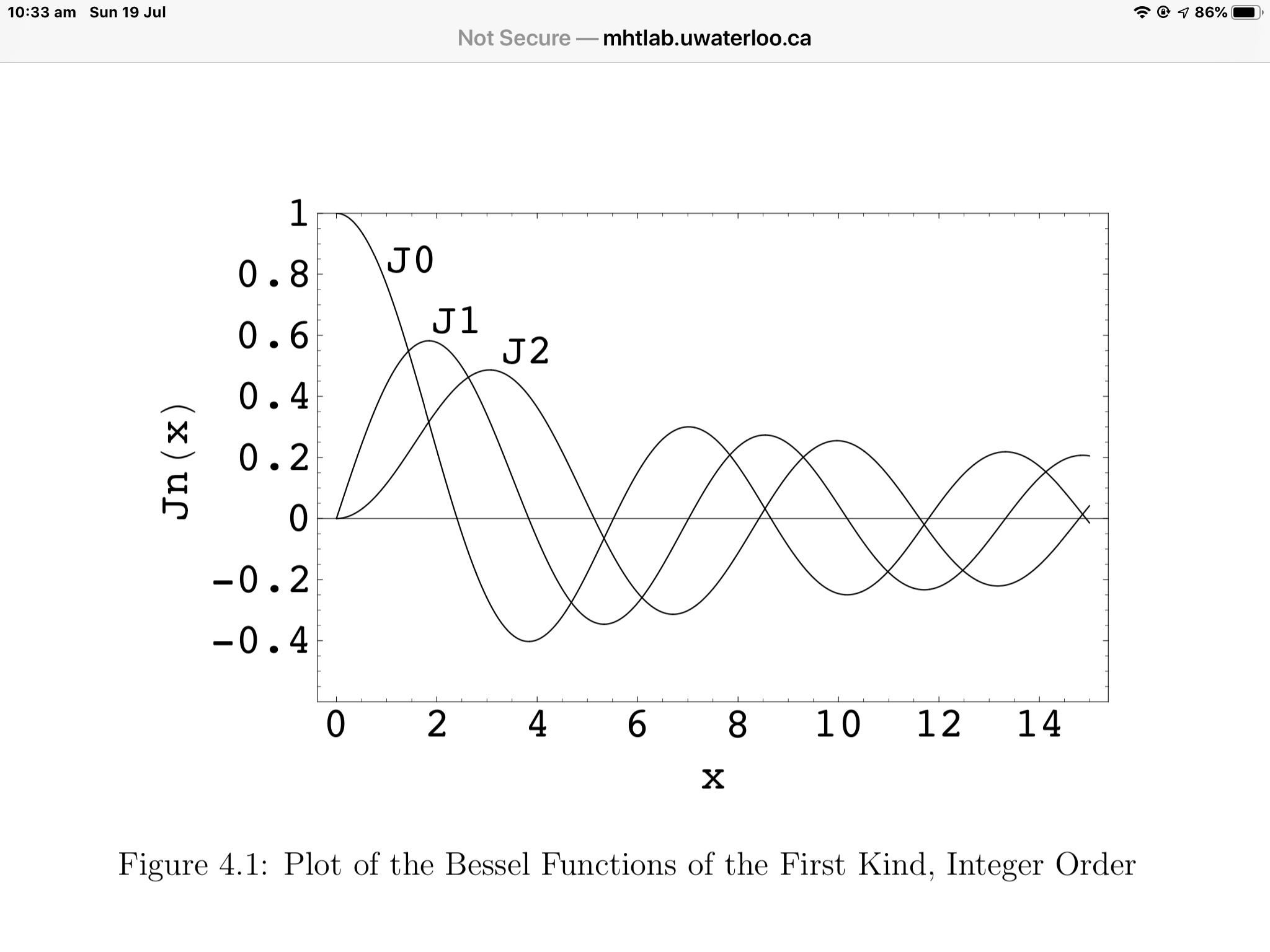
Bessel Functions
Studying this continued fraction (\(\frac{e^2+1}{e^2-1} = [1, 3, 5, 7, 9, 11...]\)) got me thinking about a continued fraction which should be even simpler: \([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]\). Surely this should be given by a common and recognisable real number? Well, how wrong I was! Welcome to the world of Bessel functions!
Gamma Functions
The factorial function is well known -
\(3! = 3 \cdot 2 \cdot 1 = 6,\)
\(4! = 4 \cdot 3 \cdot 2 \cdot 1 = 12,\)
\(n! = n \cdot (n-1) \cdot (n-2)...\)
But what happens in between? The Gamma function, represented by the Greek capital, \(\Gamma(x)=(x-1)!\) includes all values, not just the integers, and has some interesting properties - especially when you consider the half values of \(\frac{\Gamma(x)}{\sqrt(\pi)}\).
Chaos Theory and Cobweb Functions
Consider a population, say of fish in a pond. If the pond is fixed in size and limited in the amount of food which it can provide, then the population of fish cannot grow unbounded. In fact, the size of the population itself will limit the growth - as the number of fish (\(x\)) gets large, it will act to slow down the rate of population growth (\(r\)). A simple model of this situation over time is given by the relationship \[f(x)=r\cdot x\cdot (1-x)\]
But what happens next is far from simple!
Musical Continued Fractions
Suppose you had a list of numbers, for example, myList = [0, 2, 4, 5, 7, 9, 11, 12]. How might you turn each of those list elements into a musical tone - perhaps have 0 represent middle C, and each unit a semi-tone higher. 1 would be C#4, 2 D, and so on. Then myList should give the scale from middle C (C4) to the next C (C5).
Perhaps even write and play your own continued fraction music? You might try dividing a piece into parts and playing in turn with others!
And more...
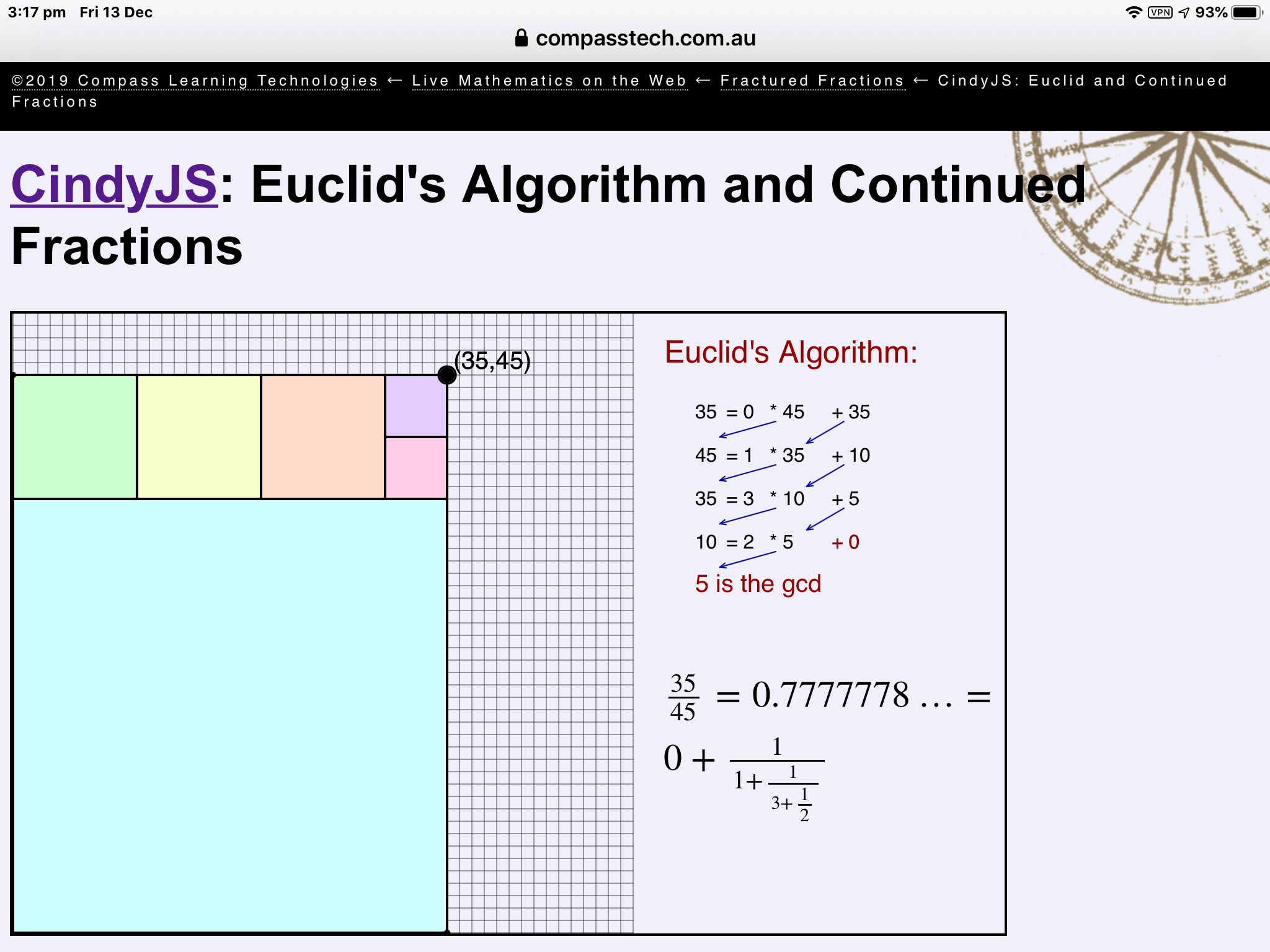
Did You Know...? There is a connection between the Euclidean algorithm for finding the greatest common divisor of two numbers and continued fractions?
Tap the image to explore.
Interested to learn more about continued fractions?
Construct your own Model with GXWeb
Build Your Own Catalan Polygons
How many non-intersecting diagonals can be drawn for each polygon?Set GXWeb Pythagorean Circles
What is the area of the inCircle for a 3-4-5 triangle?Set GXWeb Descartes Circle Theorem
Given three kissing circles of radius a, b and c (curvature \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\)) what will be the curvatures of the inner and outer kissing circles?Set GXWeb Dragon Curve/Paperfold
(In the numeric control panel, drag f slider (5 folds) from 90 to 0, then repeat for e (4 folds), d (3 folds), c (2 folds) and b (1 fold))
GXWeb Save and Share with QRCode (mp4 demo:3:02)
Test Yourself
Behind the Scenes
©2021 Compass Learning Technologies ← GXWeb Showcase ← GXWeb Jigsaws and Quizzes ← GXWeb Fractured Fractions → GXWeb Fractured Fractions Collection