©2021 Compass Learning Technologies → Live Mathematics on the Web → GXWeb Showcase → GXWeb Algebra Tiles

GXWeb Algebra Tiles

Saltire Software, home of Geometry Expressions and GXWeb

Symbolic computations on this page use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb

Meaningful Algebra with CAS and Exploring Algebra Geometrically

Algebraic Thinking Within a Technology-Rich Learning Environment

GXWeb Games and Challenges.

Explore GXWeb TakTiles

 

---

Introduction Some Concrete Examples Try the Algebra Tiles Jigsaw and GXWeb Tak Tiles Explore Algebra Tiles with GXWeb Why not Listen to your Algebra? More to Explore: The Meaningful Algebra Collection Build Your Own Models with GXWeb Behind the Scenes

 

---

---

 

Introduction

Hide

Back to Top

Jump to Model

More to Explore

Jump to GXWeb

 

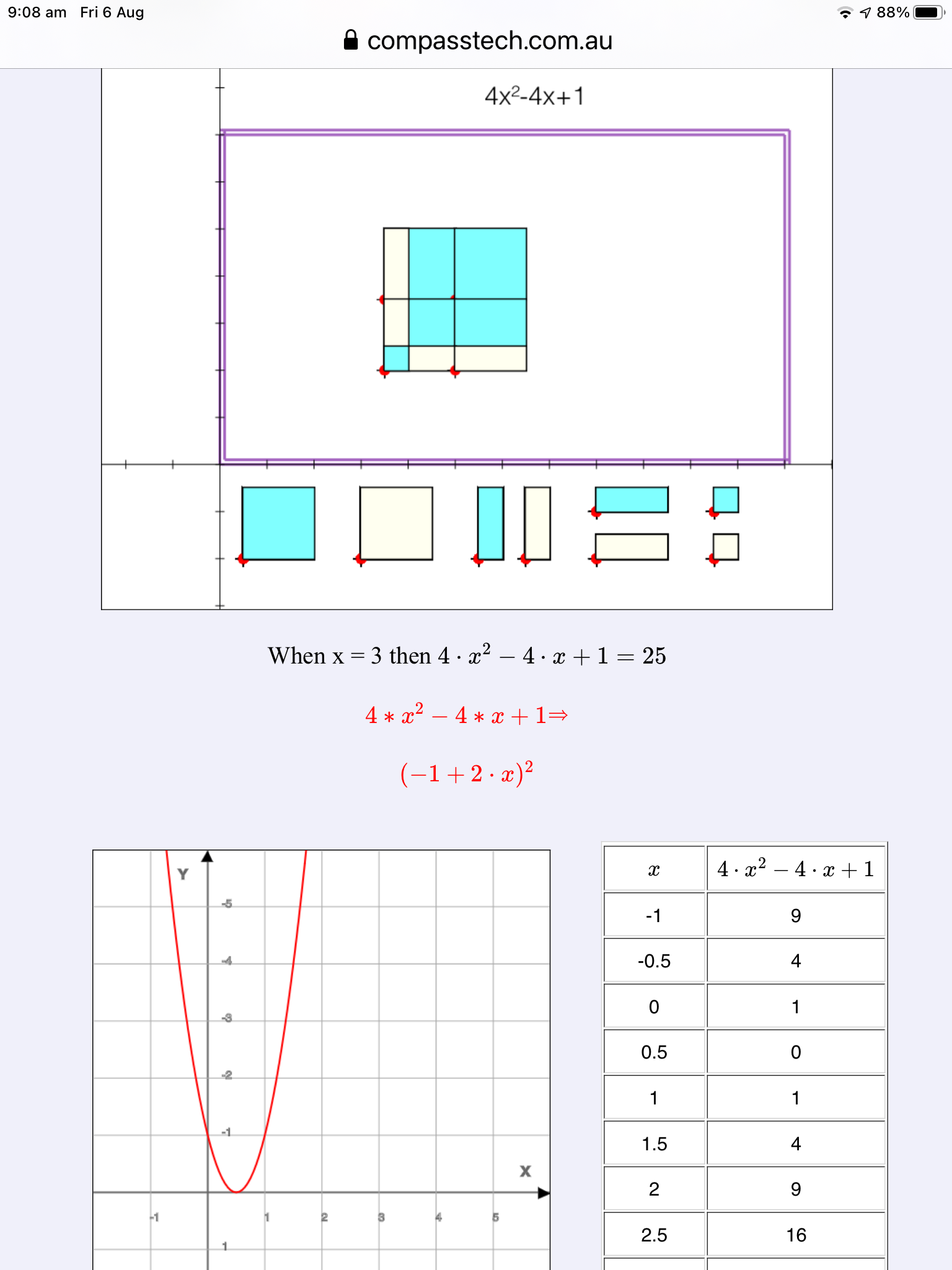
What does \(2x + 1\) mean to you? What about \(4-3x\) or even \(x^2=x+1\)

What dominant image springs to mind?

Do you see an object or a process?

Do you think of a graph? A table of values?

Students who are successful in algebra tend to have a richer repertoire of images compared to those who do not. As teachers, we need to build these images deliberately and with care.

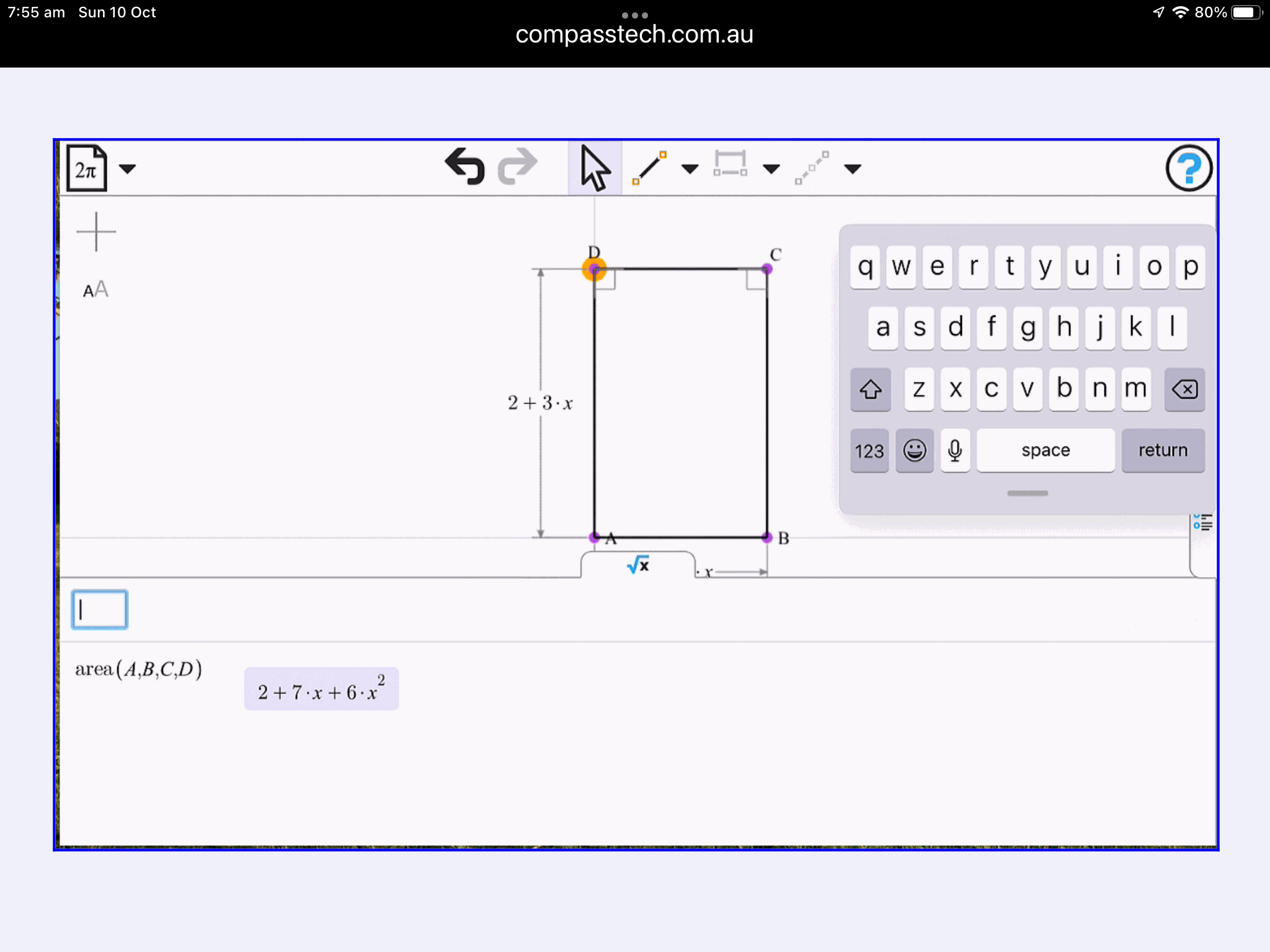
Concrete manipulatives ("algebra tiles") can be a powerful tool for building deep understanding, and the virtual variety actually offer some major advantages: they explicitly link the shapes to the symbolic form, and they establish that variables are dynamic rather than static things.

Use the tools provided here to explore multiple representations of algebraic forms - algebra tiles, along with graphs, tables of values and, of course, the symbolic form.

Hide

 

---

---

 

Some Concrete Examples

Show

Back to Top

Jump to Model

More to Explore

Jump to GXWeb

 

Drag positive and negative terms onto the table to build algebraic expressions.

 

---

 

Solving Linear Equations: In equation mode, the table is divided down the middle. Drag tiles onto each side to build your equation. Try solving linear equations by doing the same thing to each side, simplifying to get your solution. You can also use computer algebra by entering an equation into the first of the graph boxes (dragging the tiles does this automatically!) and then just press \(f(x)\) to solve it.

For example, tap on each step to solve \(3x-1=x+1\).

\[3\cdot x-1 = x + 1\]

Step 1: Add 1 to each side.

\[3\cdot x-1 + 1 = x + 1 + 1\]

\[3\cdot x = x + 2\]

Step 2: Subtract \(x\) from each side.

\[3\cdot x - x = x + 2 - x\]

\[2\cdot x = 2\]

Step 3: Divide each side by 2.

\[x = 1\]

 

---

 

Factoring Expressions: Do you know how to tell if an expression can be factored using algebra tiles? Just see if you can rearrange all the tiles to form a complete rectangle! Try some for yourself with the algebra tiles jigsaw! Think about factors of algebraic expressions: for example, consider \(3\cdot (x + 1)\), \((2\cdot x + 1)^2\) and even \((2\cdot x - 1)^2\).

Need some help with simplifying and expanding your factored expressions? GXWeb is the ideal tool! Build a rectangle. Set the sides to the two factors and ask for the area!

Hide

Back to Top

Jump to Model

More to Explore

Jump to GXWeb

---

---

 

---

---

 

Why not Listen to your algebra?

Show

Back to Top

Jump to Model

Jump to GXWeb

 

Listening to an algebraic expression offers another representation, complementing the numerical table of values, and perhaps offering new deeper insights than the visual alone.

Play ♬

Auto Play (Listen to your functions) ❌ : Set Auto Play

Show Tone Controls

261.63,293.66,329.63,349.23,392.00,440.00,493.88,523.25

Timing:

Key Signature:

Switch Views: notes <=> frequencies

---

Try Your Own Piano ⇒

Hide

 

---

 

Show

WolframAlpha: CAS+

Back to Top

Jump to Model

The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!

 

---

---

 

More to Explore: The Meaningful Algebra Collection

Hidd

Back to Top

Jump to Model

Jump to GXWeb

 

Can you see how our concrete algebra models help us to visualise and think about both simple and more interesting algebraic forms?

Continue further along this path by trying some of the assessment activities and explorations from the GXWeb Meaningful Algebra Collection, including:

Meeting a Friend ⇒ The Beach Race ⇒ The Paperfold Problem ⇒ The Case of the Diminishing Square ⇒ The Falling Ladder ⇒ and Birthday Buddies ⇒ and many more...

tasklist2[0] >br/>tasklist2[0]

These activities build practical and interesting algebraic models using real language for their algebraic relationships.

Hide

 

---

---

 

Show

Construct your own Model with GXWeb

Back to Top

Jump to Model

Hide

 

---

---

 

Show

Behind the Scenes

Back to Top

Jump to Model

More to Explore

 

---

YouTube Demonstration

---

View JavaScript GXWeb Code (gxconcrete.js)

View JavaScript Shared Code (sharedcodend.js)

View JavaScript Grapher Code (grapher.js)

View JavaScript Math Print Code (latex2math.js)

View JavaScript Music Code (play.js)

---

Learn How: Create your own GXWeb Assessment Task

Learn How 2: Take GXWeb to the Next Level

Back to Top

Jump to Model

More to Explore

---

---

 

©2021 Compass Learning Technologies ← Live Mathematics on the Web ← GXWeb Showcase ← GXWeb Algebra Tiles