GXWeb Fractured Fractions Jigsaw
Saltire Software, home of Geometry Expressions and GXWeb
Symbolic computations on this page use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb
Chaos in Numberland: The secret life of continued fractions by John D. Barrow
Explore Bill Gosper (1972): Continued Fraction Arithmetic
Calkin and Wilf (1999): Recounting the Rationals
Try the full Fractured Fractions Jigsaw
Welcome to the Fractured Fractions Jigsaw!
Begin with the JigSaw: Just rearrange the squares to fill the given rectangle, and then press INPUT (or the JIGSAW button again) to enter your answer.
Then go on and explore some of the wonderful connections between continued fractions and some surprising and important corners of mathematics. Did you know, for example, that fractions grow on trees?
With special thanks to Dr Keith Tognetti of the University of Wollongong for pointing me in the direction of these wonderful numbers and igniting in me a life-long passion.
|
|
Introduction
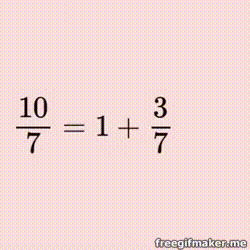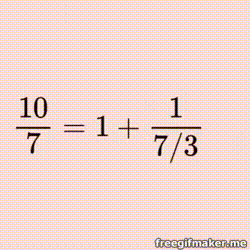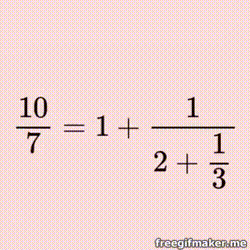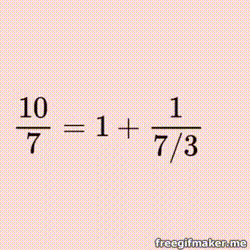
If you have not come across continued fractions in your mathematical travels, then it is high time you did!
Every real number, rational and irrational, can be represented as a continued fraction. While normal fractions can only represent rational numbers, continued fractions are different - full of surprising patterns and relationships.
Not surprisingly, rational numbers produce finite continued fractions, while irrationals become infinite continued fractions.
Unlike irrational decimals, however, even irrational continued fractions can be predictable and are an ideal way to calculate approximate values - as accurately as you like!
\[ \frac{43}{30} = 1 + \cfrac{1}{2 + \cfrac{1}{3+ \cfrac{1}{4}}} \]
\[ \pi \approx 3 + \cfrac{1}{7 + \cfrac{1}{15 + \cfrac{1}{1 + \cfrac{1}{292 + \cfrac{1}{1 + \cdots}}}}} \]
\[ e \approx 2 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1}{4 + \cfrac{1}{1+ \cdots}}}}}} \]
Continued fractions have many practical applications but one of the most important lies in their ability to offer VERY good approximations to irrational numbers - the more convergents, the better the approximation. Indeed, each convergent gives the Best Approximation of the First Kind (look that up!) AND if a large value turns up in the list, then cutting the continued fraction just before that large value gives an extremely accurate approximation!
Step-by-Step Guide to building your own continued fractions
Continued fractions do come in more than one flavour.
In most cases, we deal with SIMPLE continued fractions, for which the numerators are all equal to 1, as shown above.
The great Indian mathematician, Srinivasa Ramanujan, and other greats over many years have been fond of far more interesting varieties.
\[ \pi \approx \cfrac{4}{1 + \cfrac{1^2}{3 + \cfrac{2^2}{5 + \cfrac{3^2}{7 + \cfrac{4^2}{9 + \cfrac{5^2}{11 + \cfrac{6^2}{13 + \cdots}}}}}}} \]
\[ e \approx 2 + \cfrac{1}{1 + \cfrac{1}{2 + \cfrac{2}{3 + \cfrac{3}{4 + \cfrac{4}{5 + \cfrac{5}{6 + \cfrac{6}{7 + \cdots}}}}}}} \]
Continued fractions continue to be a source of research in many branches of mathematics. Use the tools available here to explore these wonderful mathematical opportunities!
You might notice that while simple continued fractions give predictable values for only a limited range of real numbers (the so-called Quadratic Irrationals), examples like these show that even the most transcendental of numbers can be expressed in predictable form. Observe, below, that continued fractions can also be expressed as the product of matrices!
Mathematical ToolBox
Explore Further: Continued Fractions, Farey Numbers and Fraction Trees

There are some lovely connections between continued fractions, farey numbers and fraction trees!
Did You Know that fractions grow on trees?
Or that (fraction) trees can grow from (Continued) Fractions?
Farey Trees, Stern-Brocot and Calkin-Wilf Trees offer amazing insights into the nature and structure of rational numbers, and their relationship with continued fractions.
There is even a continued fraction which generates all the rational numbers in the Farey and Stern-Brocot Sequences!
Share with Different Senses
GXWeb Jigsaws and Quizzes
QR Codes are a great way to share data and information with others, even when no Internet connection is available. Most modern devices either come equipped with QR readers in-built, or freely available.
The default link here is the GXWeb Jigsaws and Quizzes, but you can use it as an alternative to sending your assessment data via email, web or share with others in your class. You can even use it to send your own messages!
Construct your own Model with GXWeb
Behind the Scenes
©2021 Compass Learning Technologies ← GXWeb Showcase ← GXWeb Jigsaws and Quizzes ← GXWeb Fractured Fractions ← GXWeb Fractured Fractions Jigsaw
