©2023 Compass Learning Technologies → GXWeb Showcase → GXWeb Continued Fraction Collection → Continued Fractions and Magic Tables

Continued Fractions and Magic Tables

Saltire Software, home of Geometry Expressions and GXWeb

Symbolic computations on this page use the Nerdamer Symbolic JavaScript to complement the in-built computer algebra system of GXWeb.

---

Exploring the Magic Table for Continued Fractions Mathematical Toolkit An Introduction to Continued Fraction Arithmetic 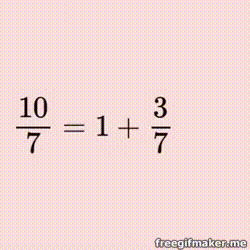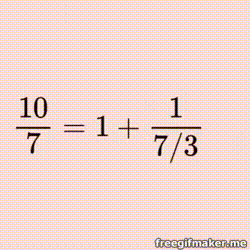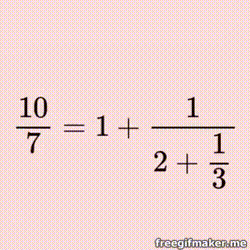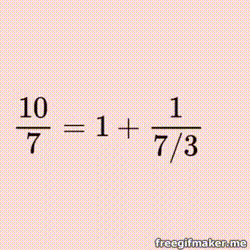Dig Deeper: Related References Behind the Scenes

 

---

---

 

Hide

Exploring the Magic Table for Continued Fractions

 

---

• Introduction: What is a Magic Table?

• Introducing the Magic Table: Dimension 1

• Explore the Magic Table in 1 Dimension

• Introducing the Magic Table: Dimension 2

• Explore the Magic Table in 2 Dimensions

• Teasing Out the Resultant Continued Fraction

• Step by Step

• General Continued Fractions: Some Examples

• Try More Examples

• Try Some Yourself

---

 

Introduction: What is a Magic Table?

To convert a real number to a continued fraction is easy! Try this yourself? But what if you want to go in the other direction? If you have a continued fraction, and would like to know the real number that it represents? For some rational numbers (and approximations of irrationals), this is (relatively) easy, since the continued fraction is finite. For most, though, it can be quite arduous. The most commonly used method involves starting from the bottom and working upwards. This approach, however, does not reveal the successive approximations, the convergents, which in many cases may be just as useful as the final result.

$$\frac{10}{7}$$ $$= 1+\frac{3}{7}$$ $$= 1 + \frac{1}{\frac{7}{3}}$$ $$= 1 + \cfrac{1}{2 + \cfrac{1}{3}}$$ $$= [1,2,3]$$

$$[1,2,3]$$ $$= 1 + \cfrac{1}{2 + \cfrac{1}{3}}$$ $$= 1 + \frac{1}{\frac{7}{3}}$$ $$= 1+\frac{3}{7}$$ $$= \frac{10}{7}$$

Alternatively, you might try the Magic Table method!

The magic table ^{1, 2} (first described by Gosper (1972) - credit for the name goes to Associate Professor Terry Gagen of the University of Sydney) offers an efficient and (relatively) simple way to generate the convergents of a continued fraction - it can even be used, in 1 or 2 dimensions, on linear fractional transformations of continued fractions and, in 3 dimensions, forms the basis for Gosper's algorithm for continued fraction arithmetic.

For example, the continued fraction of

$$\sqrt(37) =>$$ $$a(n) = [6,12,12,12,12,12,12,...]$$ $$b(n) = [1,1,1,1,1,1,1...]$$ $$6 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12 + \cfrac{1}{12... }}}}}}}$$

Using the approaches described here is much simpler than, for example, matrix methods to calculate a result such as

$$\frac{\sqrt{37} + 4}{7} = \begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \cdot \sqrt(37) = \begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \cdot \begin{bmatrix} \sqrt(37) && 0 \\ 0 && 1 \end{bmatrix}$$

where the linear fractional transformation is the matrix

$$\begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \ and \ \begin{bmatrix} 1 && 0 \\ 0 && 1 \end{bmatrix}$$

represents the identity matrix.

Magic Table Index

Jump to MathBox

 

---

 

$$...$$	$$12$$	$$12$$	$$12$$	$$12$$	$$12$$	$$6$$	$$a(n)$$
$$...$$	$$1$$	$$1$$	$$1$$	$$1$$	$$1$$	$$(1)$$	$$b(n)$$
$$...$$	$$213442$$	$$17665$$	$$1462$$	$$121$$	$$10$$	$$1$$	$$4$$
$$...$$	$$148183$$	$$12264$$	$$1015$$	$$84$$	$$7$$	$$0$$	$$7$$

 

---

 

Show

Introducing the Magic Table: Dimension 1

 

Gosper's original (dimension 1) version of the magic table was presented horizontally, reading from right to left. A simplified form (which delivers each convergent in turn) might be represented as shown above.

Note that Gosper dealt only with simple continued fractions for which all b(n) (numerator) terms may be assumed to be 1. We go a step further here, adding a b(n) row to support general continued fractions.

Can you see how the pairs of numbers below the continued fraction terms are calculated? (Notice that the first convergent is calculated directly from the terms of the linear fractional transformation.)

Tap on these pairs to see, or tap on the red continued fraction terms - from right to left - to see Gosper's Magic Table in action!

 

Explore the Magic Table in 1 dimensionTry Yourself

Magic Table Index

Jump to MathBox

 

---

Show

Introducing the Magic Table: Dimension 2

 

More importantly, Gosper was not really interested in simply outputting the convergents of continued fractions.

His real goal was to take a continued fraction, operate on it in some way - initially, using a linear fractional transformation, but leading to arithmetic operations with another continued fraction - and output the result directly as a continued fraction: true continued fraction arithmetic!

For this, he needed more dimensions for his magic table!

 

Explore the Magic Table in 2 dimensions Try Yourself

RESET ALL

 

---

Show

Teasing Out the Resultant Continued Fraction

 

It should be noted that drawing out each term of the resultant continued fraction is not always a straightforward operation.

Consider the first TWO convergents of

$$\frac{\sqrt{37} + 4}{7} = \begin{bmatrix} 1 && 4 \\ 0 && 7 \end{bmatrix} \cdot \sqrt(37)$$ $$=> \frac{10}{7} \ and \ \frac{121}{84}$$

Taking the floor or integer part of both delivers the same result ($|\frac{10}{7}| = |\frac{121}{84}| = 1$), so we can be confident in the first term of our resultant continued fraction.

To continue, we need the dimension 2 table, since we now move one step down and one step to the left (in the table above, or to the right in the table below). The next two convergents to consider are $\frac{84}{37}$ and $\frac{1015}{447}$. If the floor values of both agree (which they do in this case), we continue this process, moving down and horizontally forward.

If NOT, then we simply move one step horizontally forward, and try the next pair of convergents, until we find two that agree, and this process gives each subsequent term of our resultant continued fraction.

For a more interesting example, consider Gosper's case of $e$ with linear fractional transformation, [1,-1,1,1]:

$$tanh(\frac{1}{2}) = \frac{e-1}{e+1}$$

Here we see that the first convergent pair ($\frac{1}{3}$ and $\frac{2}{4}$) both deliver floor values of 0. The second pair ($\frac{11}{5}$ and $\frac{4}{2}$) give us the next resultant term of 2.

Subsequently, though, $|\frac{5}{1}| = 5$ and $|\frac{7}{1}| = 7$. We must continue to the next terms, $\frac{12}{2}$ and (with a little calculation) $\frac{55}{9}$ ($4 \cdot 12 + 1 \cdot 7 = 55$ and $4 \cdot 2 + 1 \cdot 1 = 9$) to confirm the floor result of 6.

The floor values of pairs of adjacent convergents must differ by no more than 1 to deliver the next term of the resultant continued fraction.

Magic Table Index

Jump to MathBox

 

---

---

For ease of presentation, in our versions, the terms are displayed vertically, with the terms of the linear fractional transformation found at the top of the numerator and denominator columns (rotated -90°).

Magic Table Index

Jump to MathBox

 

---

Show

Step by Step

 

Tap to view: Simple Convergent Form 1 Simple Convergent Form 2   Gosper Magic Table 1 Gosper Magic Table 2 Gosper Magic Table 3 Gosper Magic Table 4 Gosper Magic Table 5	In its simplest form, Gosper's Magic Table initially offers a convenient way to generate the convergents for a given continued fraction, along with a linear fractional transformation, expressed as a 2x2 matrix. (Tap for an example) ⇑

Magic Table Index

Jump to MathBox

 

---

Show

General Continued Fractions: Some Examples

 

Note that the Magic Table presented here represents an extension of Gosper's method, supporting general continued fractions in addition to simple ones. For example, did you know that

$$\pi \approx 0 + \cfrac{4}{1 + \cfrac{1}{3 + \cfrac{4}{5 + \cfrac{9}{7 + \cfrac{16}{9 + \cfrac{25}{11 + \cfrac{36}{13 + \cfrac{49}{15 + \cfrac{64}{17 + \cfrac{81}{19...}}}}}}}}}}$$ $$a(n) = [0,1,3,5,7,9,11,13,15,17,19]$$ $$b(n) = [4,1,4,9,16,25,36,49,64,81]$$

---

---

And what about the Farey and Stern-Brocot Continued Fractions: if you wanted to start a list of every rational number, then these amazing continued fractions are perfect for that!

$$0 + \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1}}}} = 0 + \cfrac{1}{3 + \cfrac{1}{-1 + \cfrac{1}{3 + \cfrac{1}{-1}}}}$$ $$⇒ [0,\frac{1}{3},\frac{1}{2},\frac{2}{3},1]$$	Farey Sequence Level 3: mtable([[0,3,-1,3,-1],[1,1,1,1,1]],[1,0,0,1]) OR mtable([[0,3,1,3,1],[1,-1,-1,-1,-1]],[1,0,0,1])
$$0 + \cfrac{1}{4 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{5 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1}}}}}}}}$$ $$⇒ [0,\frac{1}{4}, \frac{1}{3}, \frac{2}{5},\frac{1}{2}, \frac{3}{5}, \frac{3}{4}, \frac{2}{3},1]$$	Farey Sequence Level 4: mtable([[0,4,-1,3,-1,5,-1,3,-1],[1,1,1,1,1,1,1,1,1]],[1,0,0,1]) OR mtable([[0,4,1,3,1,5,1,3,1],[1,-1,-1,-1,-1,-1,-1,-1,-1]],[1,0,0,1])
$$0 + \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{5 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1}}}}}}}}$$ $$⇒ [0,\frac{1}{3},\frac{1}{2},\frac{2}{3},1,\frac{3}{2},\frac{2}{1}, \frac{3}{1},\frac{1}{0}]$$	Stern-Brocot Sequence Level 3: mtable([[0,3,-1,3,-1,5,-1,3,-1],[1,1,1,1,1,1,1,1,1]],[1,0,0,1]) OR mtable([[0,3,1,3,1,5,1,3],[1,-1,-1,-1,-1,-1,-1,-1]],[1,0,0,1])

---

Stern-Brocot Sequence Level 4:

$$0 + \cfrac{1}{4 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{5 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{7 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1 - \cfrac{1}{5 - \cfrac{1}{1 - \cfrac{1}{3 - \cfrac{1}{1}}}}}}}}}}}}}}}}$$ $$⇒ [0,\frac{1}{4}, \frac{1}{3}, \frac{2}{5},\frac{1}{2}, \frac{3}{5}, \frac{3}{4}, \frac{2}{3},1, \frac{3}{2}, \frac{4}{3}, \frac{5}{3},\frac{2}{1}, \frac{5}{2}, \frac{3}{1}, \frac{4}{1}, \frac{1}{0}]$$

 

mtable([[0,4,-1,3,-1,5,-1,3,-1,7,-1,3,-1,5,-1,3],[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]],[1,0,0,1],0,17)

OR

mtable([[0,4,1,3,1,5,1,3,1,7,1,3,1,5,1,3],[1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]],[1,0,0,1],0,17)

Magic Table Index

Jump to MathBox

---

---

Show

Try More Examples

 

Simple (Convergent) Magic Table Dimension 1	Gosper Magic Table Dimension 2
Enter mtable(), or mtable(sqrt(37)), or mtable(sqrt(37),[1,4,0,7]), or even mtable(sqrt(37),[1,4,0,7],0,12) Try one of Gosper's examples: mtable(sqrt(2),[0,2,-1,3],0,12) You can also enter arrays: mtable([1,2,3,4,5],[1,0,0,1],0,12) or mtable([[1,2,3,4],[4,3,2,1],[1,0,0,1],0,12) Try mtable([[2,1,2,3,4,5,6,7,8,9,10],[1,1,2,3,4,5,6,7,8,9,10]],[1,0,0,1],0,12)	Enter gmt(), or gmt(sqrt(37)), or gmt(sqrt(37),[1,4,0,7]), or even gmt(sqrt(37),[1,4,0,7],0,12) Try one of Gosper's examples: gmt(sqrt(2),[0,2,-1,3],0,12) You can also enter arrays: gmt([1,2,3,4,5],[1,0,0,1],0,12) or gmt([[1,2,3,4],[4,3,2,1],[1,0,0,1],0,12) Try gmt([[2,1,2,3,4,5,6,7,8,9,10],[1,1,2,3,4,5,6,7,8,9,10]],[1,0,0,1],0,12)

mtable([[0,1,3,5,7,9,11,13,15,17,19],[4,1,4,9,16,25,36,49,64,81,100]],[1,0,0,1],0,12).

Perhaps even compare
mtable([[4,2,2,2,2,2,2,17,294],[-1,-1,-1,-1,-1,-1,-1,-1,-1]],[1,0,0,1]) with
mtable([[4,-2,2,-2,2,-2,2,-17,294],[1,1,1,1,1,1,1,1,1]],[1,0,0,1])?

---

 

Try Some Yourself

Magic Table Index

 

---

 

Hide

 

---

---

 

Magic Table Index

 

$$f$$

$$f(x)$$

More MathBoxes

---

 

$$g$$

$$g(x)$$

$$h$$

$$h(x)$$

RESET
ALL Numeric
ToolKit CAS
ToolKit Play
♬

Graph Table Steps Axes TextBoxes Sliders

---

---

Back to Top

This document requires an HTML5-compliant browser.

$a =$					▶
		-1	5	1
$b =$					▶
		-1	5	1
$c =$					▶
		-1	5	1
\\(d\\)				▶
	-1	0	5
\\(e\\)				▶
	-1	0	5

App generated by GXWeb

Show More Tools

 

---

---

 

Show Spreadsheet

Continued Fraction Spreadsheet Explorer

This browser-based spreadsheet uses the handsontable JavaScript library.

 

43/30 Phi Pi Pi+ e e+

Show/Hide Convergents Plot

Hide Spreadsheet

Back to Top

Jump to MathBox

 

---

 

Show Wolfram Alpha

WolframAlpha: CAS+

 

Sometimes, to deal with those stubborn, hard to reach problems, you need something stronger! The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!

Submit Build your own widget »Browse widget gallery »Learn more »Report a problem »Powered by Wolfram|Alpha Terms of use Share a link to this widget: More Embed this widget »

Hide Wolfram Alpha

Back to Top

Jump to MathBox

   

---

 

GeoGebra

GeoGebra offers another fast and accurate CAS alternative. You may also like to explore the GeoGebra web app.

Back to Top

Jump to MathBox

Timing: Key Signature:

Play ♬

Switch Views: notes <=> frequencies

 

---

---

 

Hide QR

Share with QR Code

Back to Top

Jump to MathBox

QR Codes are a great way to share data and information with others, even when no Internet connection is available. Most modern devices either come equipped with QR readers in-built, or freely available. The default link here is the GXWeb Jigsaws and Quizzes, but you can use it as an alternative to sending your assessment data via email, web or share with others in your class. You can even use it to send your own messages!

GXWeb Jigsaws and Quizzes Send Your Own QR Code Reset QR Code

Send Web Address ⇑

Hide QR

 

---

Show Results

Share Your Results

Back to Top

Jump to MathBox

 

Enter your name:	? Abel, Nils Agnesi, Maria Bernoulli, Daniel Cantor, Georg Descartes, Rene Euler, Leonhard Fermat, Pierre Galois, Evariste Germain, Sophie Hypatia Johnson, Katherine Liebniz, Gottfried Lovelace, Ada Monge, Gaspard Newton, Isaac Noether, Emmy Pythagoras Ramanujan, Srinivasa Riemann, Bernhard Sylvester, James Tao, Terence Weierstrass, Karl' Zeno
My class:
Email to:

Session report length: 0 characters.

⇒ Web

⇒Email

Clear

Back to Top

Jump to MathBox

Hide Results

Hide More Tools

---

 

 

Back to Top

Jump to MathBox

Timing: Key Signature:

Play ♬

Switch Views: notes <=> frequencies

 

---

---

 

Show

Continued Fraction Arithmetic

Contrary to everybody, this self contained paper will show that continued fractions are not only perfectly amenable to arithmetic, they are amenable to perfect arithmetic. (Bill Gosper, 1972)

For Gosper, the appealing concept of perfect arithmetic may well have involved using continued fractions to perform calculations to any desired degree of accuracy. Continued fractions are ideal tools for successive approximation.

The examples explored here may offer a glimpse into one of the enduring questions regarding continued fractions: they are wonderful at representing numbers, both rational and irrational, but can they also serve as practical tools for computation?

While some of these examples involve simple, finite rational values, it is unlikely that anyone would realistically wheel in continued fraction arithmetic for such questions as $\frac{10}{7} + \frac{22}{5}$.

But for those convoluted rationals and especially those infinite irrationals? Well... it was made for such as these!

Gosper
Method Matrix
Method

A Quick Overview

GXWeb Continued Fraction Arithmetic ⇒

Hide

Back to Top

Magic Table Index

Mathematical ToolBox

 

---

---

 

Show

Dig Deeper: Related References

• GXWeb Continued Fraction Collection

• GXWeb Fractured Fractions

• GXWeb Fractured Functions

• GXWeb Dragons, Folds and Fractions

• GXWeb Continued Fraction Arithmetic

• Extending Stern Brocot and Continued Fractions

• Unpacking Continued Logarithms

---

Bill Gosper (1972) Appendix 2: Continued Fraction Arithmetic.

Rosetta Code: Continued Fraction Arithmetic.

Continued Fraction Arithmetic

An Introduction to Continued Fractions by Dr Ron Knott

Continued Fractions by Ben Lynne

Arithmetic with...Continued Fractions?? (YouTube)

---

GXWeb Dragons, Folds and Fractions (YouTube)

A Quick Paperfold (YouTube)

The Summed PaperFolding Sequence (YouTube)

---

Hide

Back to Top

Magic Table Index

Mathematical ToolBox

 

---

---

 

Show

Behind the Scenes

Back to Top

Magic Table Index

Mathematical ToolBox

 

View JavaScript GXWeb Code (gxmathbox.js)

View JavaScript Latex2Jath Code (latex2mth.js)

View JavaScript Shared Code (sharedcodend.js)

Back to Top

Magic Table Index

Mathematical ToolBox

---

---

 

©2023 Compass Learning Technologies ← GXWeb Showcase ← GXWeb Continued Fraction Collection ← Continued Fractions and Magic Tables