©2025 Compass Learning Technologies ← GXWeb Showcase → GXWeb Harmonic Playground
GXWeb Harmonic Playground
Saltire Software, home of Geometry Expressions and GXWeb
Symbolic computations on this page use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb
|
|
Introducing the Harmonic Series
The harmonic series is the divergent infinite series formed by the sum of the reciprocals of the positive integers. Graphically, this is the area under the function \(\frac{1}{floor(1+x)}\).
\[H(n) = \sum_{k = 1}^{n} \frac{1}{k} = \int_{0}^{n}(\frac{1}{floor(1+x)})dx\]\[H(n) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + ... + \frac{1}{n}\]The terms are in harmonic progression: each term after the first two is the harmonic mean of its neighbours.
\[...a,b,c... \]\[b = \frac{2 \cdot a \cdot c}{(a + c)} \]\[b = \frac{2}{(\frac{1}{a} + \frac{1}{c})}\] \[...\frac{1}{n-1}, \frac{1}{n}, \frac{1}{n+1}... \]\[\frac{1}{n} = \frac{2 \cdot (\frac{1}{n-1}) \cdot (\frac{1}{n+1})}{(\frac{1}{n-1} + \frac{1}{n+1})} \]\[\frac{1}{n} = \frac{2}{(n-1) + (n+1)}\] The sum to \(n\) terms of the harmonic series may be calculated by adding Euler's Gamma Constant \(\gamma\) and the \(n\)th natural logarithm:
\[H(n) = \gamma + log(n)\]\[For \ example,\]\[H(1000) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} +...+ \frac{1}{1000}\]\[where\]\[\gamma = 0.5772156649\]\[+\]\[log(1000) = 0.5772156649 + 6.907755278982137\]\[\approx 7.485470860550343\]
Euler's Gamma Constant
TheEuler-Mascheroni Constant \(\gamma\), sometimes also called 'Euler's constant' or 'the Euler constant' (but not to be confused with the constant \(e=2.71828182845904523...\) or with its versatile cousin, the Gamma Function \(\Gamma\)) is defined as the limiting difference between the sum and integral of \(\frac{1}{x}\) or between the harmonic series and the natural logarithm. (OEIS A001620)
\[\gamma = \lim_{n \to \infty} \left \{ \sum_{k = 1}^{n} \frac{1}{k} - \int_{k=1}^{n}{\frac{1}{k}}dk \right \} = \lim_{n \to \infty} \left \{ \sum_{k = 0}^{n} (\frac{1}{1+k}) - \int_{k=0}^{n}{(\frac{1}{1+k})}dk \right \}\]\[\gamma = \lim_{n \to \infty} \left \{ \sum_{k = 1}^{n} \frac{1}{k} - ln(n) \right \} = \lim_{n \to \infty} \left \{ \sum_{k = 0}^{n} (\frac{1}{1+k}) - ln(1+n) \right \} \]\[\gamma = \lim_{n \to \infty} \left \{ H(n) - ln(n) \right \}\]\(\gamma\) occurs in many integrals. In fact, it is considered by some to be the next most commonly occurring constant, after \(\pi\) and \(e\)!
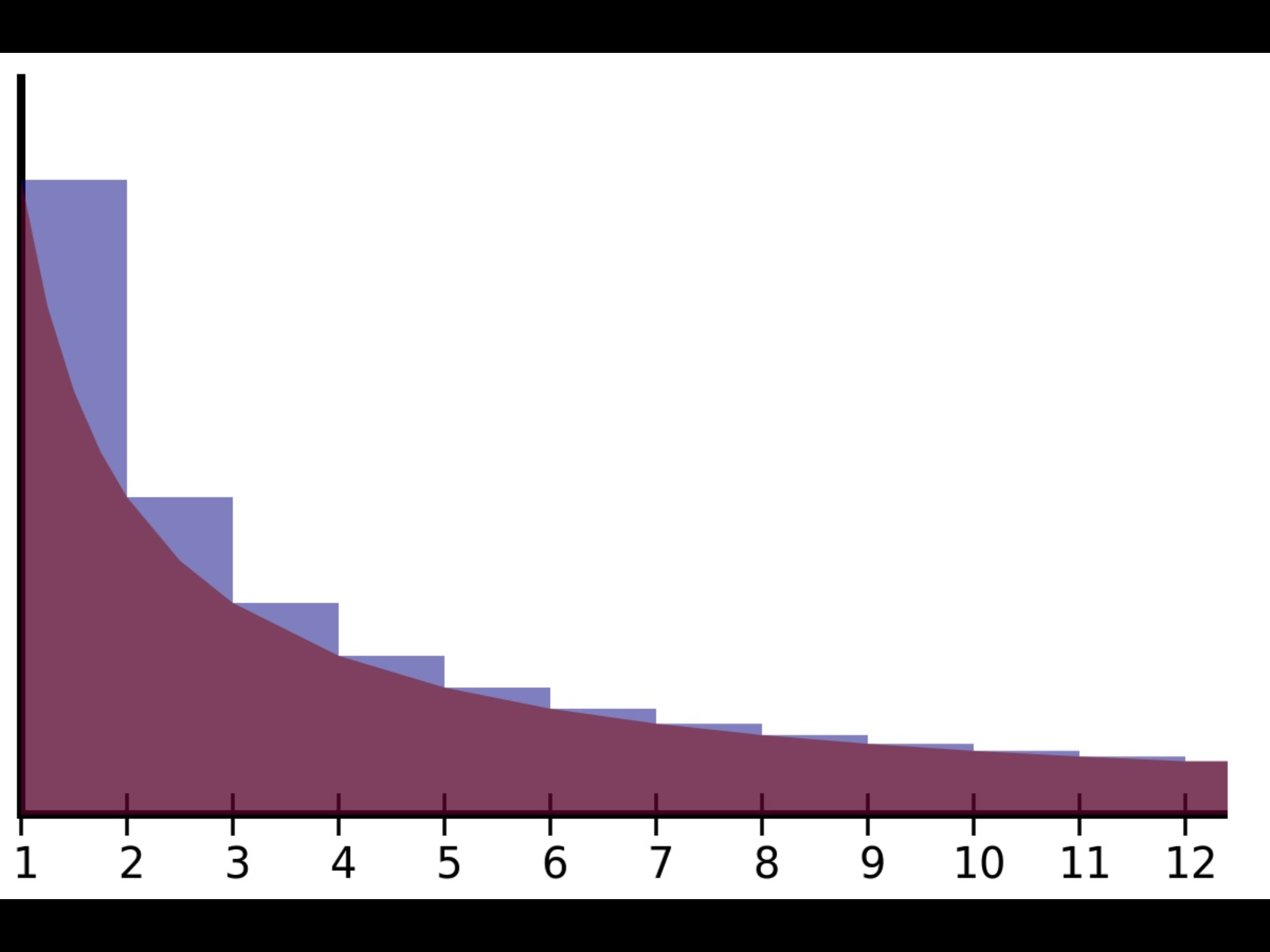
Graphically, it may be observed as the difference between the areas under the harmonic series
\[H(n) = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} +...\]\[and \ \frac{1}{x+1}\]Curiously, it is still not known if this constant is irrational, let alone transcendental.
The area of the blue region converges to Euler's constant.
Exploring the Harmonic Continued Fractions
As a result of the work of University of Wollongong mathematicians, Martin Bunder, Peter Nickolas and Joseph Tonien (2017, 2019, 2020) and building upon the work of Euler and others, the Harmonic Series may also be expressed in the form of continued fractions - an infinite number of continued fractions, in fact!
They note that, by the Seidel-Stern Theorem, since the harmonic series \(\sum{\frac{1}{n}}\) diverges, then for any positive real number \(t\) the harmonic continued fractions HCF(t) will converge.
\[HCF(t) = \frac{t}{1} + \cfrac{1}{\frac{t}{2} + \cfrac{1}{\frac{t}{3} + \cfrac{1}{\frac{t}{4} + \cfrac{1}{\frac{t}{5} + \cfrac{1}{\frac{t}{6} + \cfrac{1}{\frac{t}{7} + \cfrac{1}{\frac{t}{8} + \cdots }}}}}}}\] \[ and \ equivalent \ form\] \[HCF(t) = t + \cfrac{1\cdot 2}{t + \cfrac{2\cdot 3}{t + \cfrac{3\cdot 4}{t + \cfrac{4\cdot 5}{t + \cfrac{5\cdot 6}{t + \cfrac{6\cdot 7}{t + \cfrac{7\cdot 8}{t + \cdots }}}}}}}\]
When t = 1, after 100 steps,
\[\frac{1}{1} + \cfrac{1}{\frac{1}{2} + \cfrac{1}{\frac{1}{3} + \cfrac{1}{\frac{1}{4} + \cfrac{1}{\frac{1}{5} +\cdots + \cfrac{1}{\frac{1}{100}}}}}}\] \[ \approx 1.7519968891863615\]Exact result for HCF(1):
\[\frac{2}{(\pi-2)} = 1.7519383938841089\] \[Error \approx 0.0034762\%\]
When \(t = 1\) the first few convergents of the harmonic continued fraction HCF(1) are
[1,3,\(\frac{9}{7}\),\(\frac{45}{19}\),\(\frac{75}{53}\),\(\frac{175}{81}\),\(\frac{1225}{823}\),\(\frac{11025}{5359}\),\(\frac{19845}{12923}\),\(\frac{43659}{21877}\),\(\cdots \)]
Dive Deeper into the Harmonic Continued Fractions
References
Mathematical Toolkit
A Search for Harmony
Many (many) years ago I became intrigued by a curious and (relatively) little known fellow called the harmonic mean. Although in schools these days we only hear about the arithmetic and geometric means, historically there were scattered references, all the way back to Pythagoras.
The harmonic mean seemed to appear in those annoying problems that just did not seem to behave the way we expect them to - they were counter-intuitive! This was a great indicator of something worthy of further investigation - anything that shakes our complacency (and that of our students) is a great place to start in engaging them.
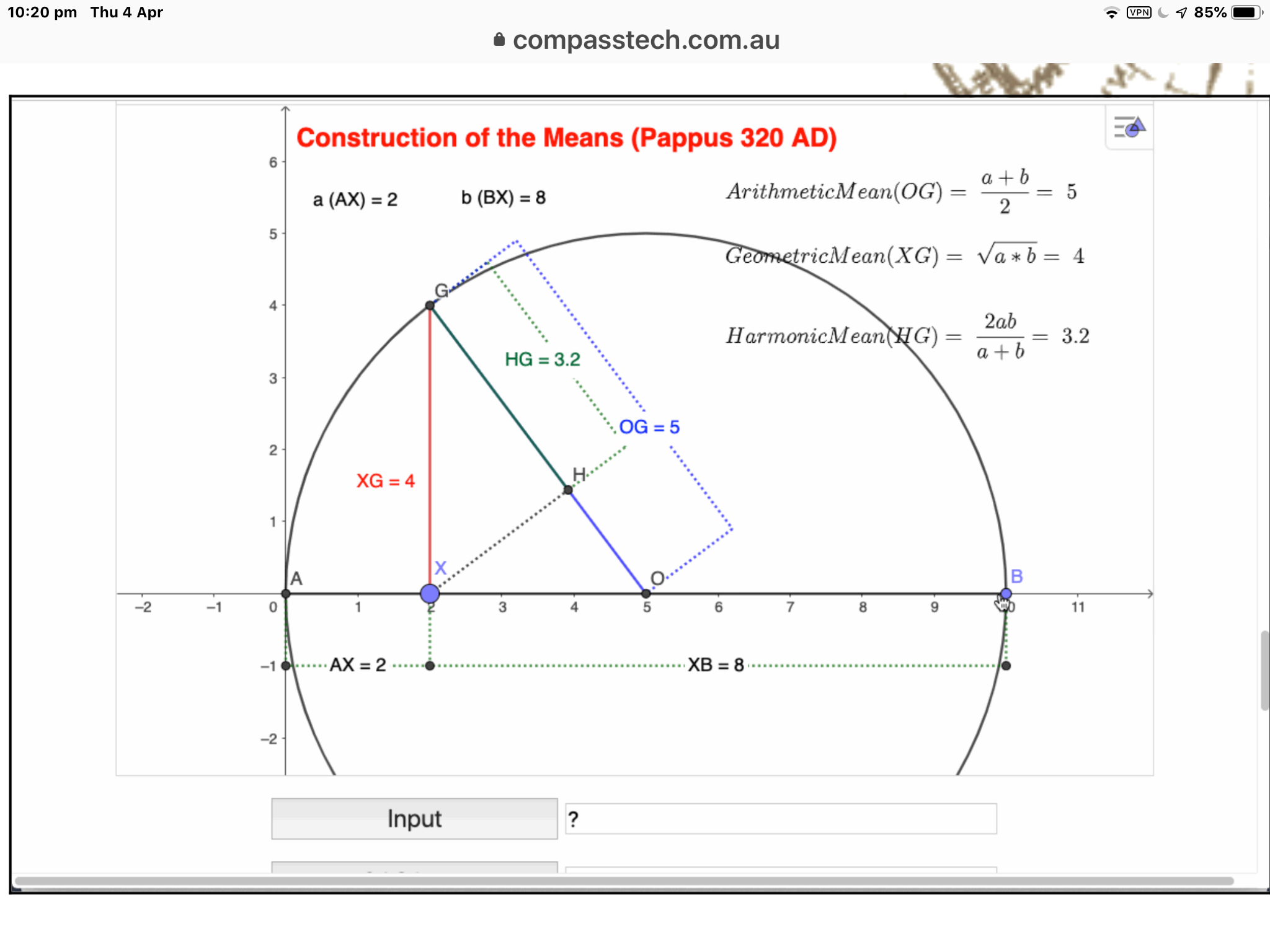
So two questions began to drive my interest: what does the harmonic mean have to do with music? and what does the harmonic mean look like? (since the mathematics of the Greeks was largely visual and geometric, if they knew of this mean, then they knew how to construct it - but I could not easily find such a construction).
My search eventually led me literally to the bowels of the University of Sydney mathematics library and a very old book, where interesting discoveries awaited!
What is the "harmonic mean"?
How is it related to its more famous cousins?
What does it have to do with music?
To the Greeks, mathematics was largely visual - so how might Pythagoras have constructed the Harmonic Mean?
Is it of any practical use today?
When teaching this activity, I would have students measure and listen to different scales using varying string lengths (or finger positions) on guitars (which are actually not as good for this purpose as instruments such as violins, which have no frets!).
I recently discovered that there are easily available tone generators for web browsers on any platform. What a great way to make this topic come to life!
For an extensive online exploration of this fascinating topic, visit Harmonic Mathematics