©2021 Compass Learning Technologies → Live Mathematics on the Web → Geometry Expressions Showcase → GXWeb Apollonian Gaskets and Mathematical Bubbles

GXWeb Apollonian Gaskets and Mathematical Bubbles

Saltire Software, home of Geometry Expressions and GXWeb

Symbolic computations on this page use Nerdamer Symbolic JavaScript to complement the in-built CAS of GXWeb

GXWeb Kissing Circles Challenge

GXWeb Farey Numbers and Kissing Circles

The Arbelos: Shoemakers' Knives and Kissing Circles

Descartes' Kissing Circles Theorem

A Tisket, a Tasket, an Apollonian Gasket

Circular Reasoning and Apollonian Gaskets and Code Golf!

 

---

Introduction Revisiting Descartes Seeking Your Centre Explore Apollonian Bubbles with GXWeb Apollonian Gasket Spreadsheet Explorer Mathematical ToolBox WolframAlpha: CAS+ Build Your Own Model with GXWeb Behind the Scenes

 

---

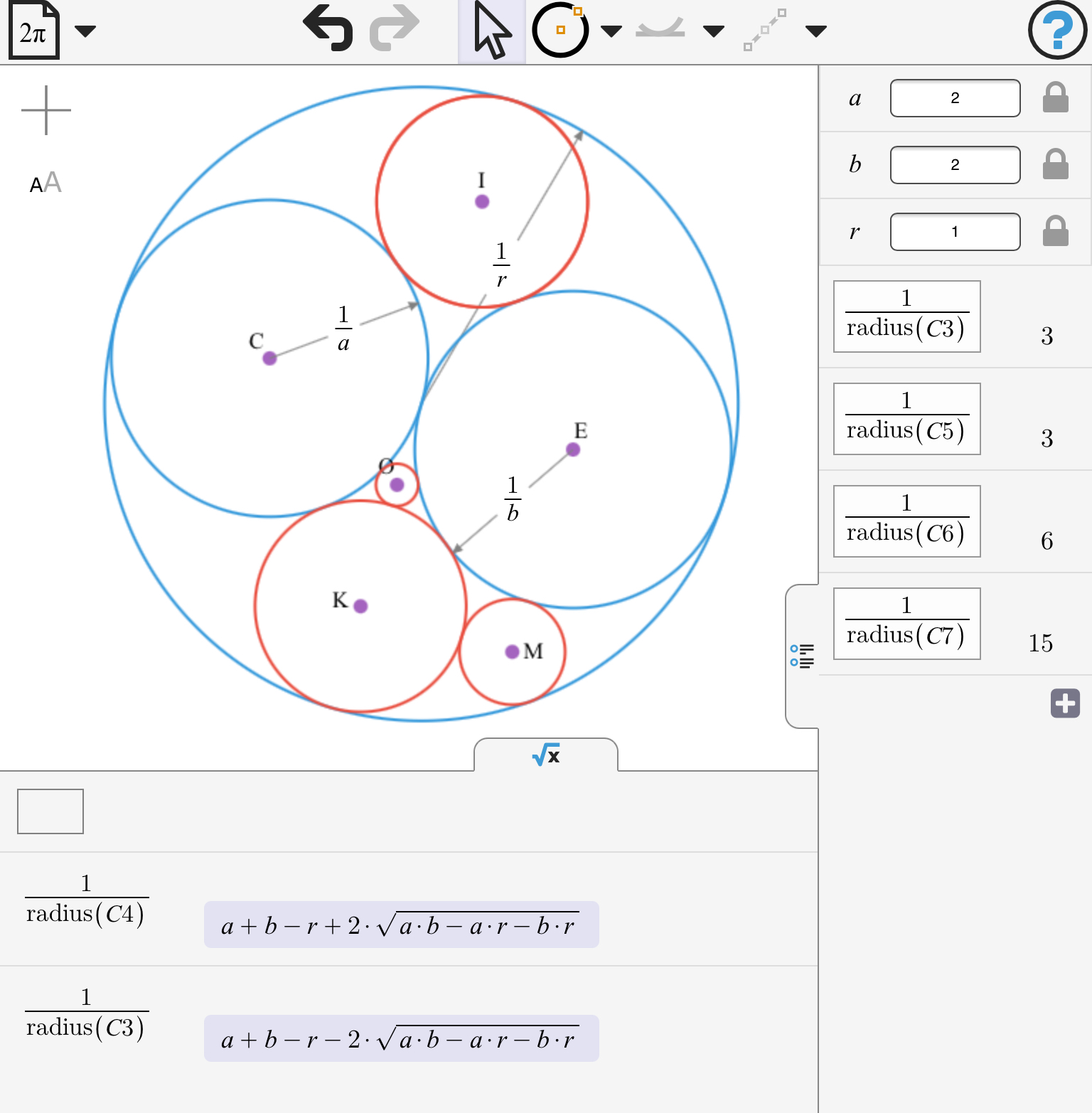
The Kiss Precise For pairs of lips to kiss maybe Involves no trigonometry. 'Tis not so when four circles kiss Each one the other three. Four circles to the kissing come The smaller are the benter. The bend is just the inverse of The distance from the center. Though their intrigue left Euclid dumb, There's now no need for rule of thumb. Since zero bend's a dead straight line, And concave bends have minus sign, The sum of the squares of all four bends Is half the square of their sum. Frederick Soddy (1936) Use this model to explore some of the many integral gaskets and their curvatures...

---

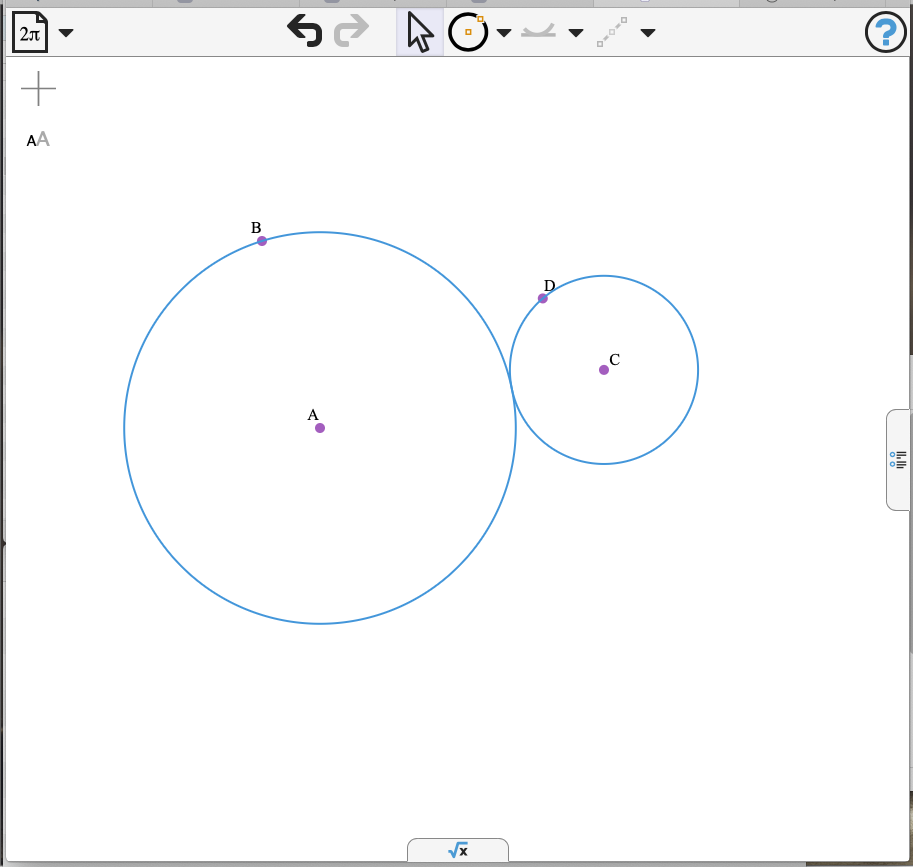
Imagine two circles - kissing! Now add a third circle to kiss both of these - it can only be placed in one of THREE positions, but could have many different sizes. Once the third kissing circle is added, however, everything changes! Any further kissing circles are fully determined - they may only lie in certain positions and their sizes (radii OR their reciprocals, curvatures or bends) are fixed. In fact, given any THREE kissing circles, there are only TWO possible subsequent circles - a feature which Descartes recognised as quadratic! Before proceeding, you might like to take a moment and try the GXWeb Kissing Circles Challenge

⇑ Tap for more...

---

Did you know...

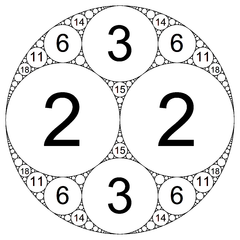
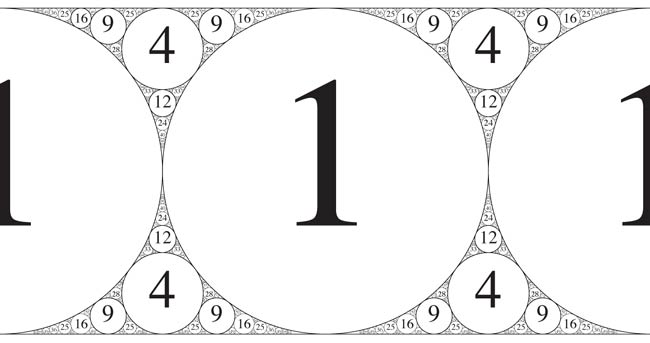
• If the first four curvature values of an Apollonian Gasket are INTEGERS, then all subsequent circles will have whole number values?!

• For any integer n > 0, there exists an Apollonian gasket defined by the following curvatures: \[[-n, n + 1, n(n + 1), n(n + 1) + 1]\] For example, the gaskets defined by (-2, 3, 6, 7), (-3, 4, 12, 13), (-8, 9, 72, 73), and (-9, 10, 90, 91) all follow this pattern.

---

Show

Introduction

Index

Back to Top

Jump to Model

Mathematical ToolBox

Jump to GXWeb

A gasket is a mechanical seal which fills the space between two or more joined surfaces. An engineer or mechanic designing a gasket will put just the right number of holes to do the job required. Put the design into the hands of a mathematician and you will instead end up exploring just how many circles can be fitted into the available space - and, of course, what patterns emerge in squeezing them together like the bubbles in a bubble bath! The mathematically-inclined have been fascinated with kissing circles for centuries. Apollonius of Perga from the third century BC is credited with laying the foundations for our Apollonian Gaskets. Some two thousand years later, Descartes discovered that, for any three circles tangent to each other, two other circles exist (one inner and the other bounding the three) and all are related by a quadratic equation. This relationship is described most easily in terms of the curvature of each circle, where curvature is defined as the inverse of the radius.

Descartes' Kissing Circles

Farey Numbers and Ford Circles

Hide ⇑

 

---

 

Show

Revisiting Descartes

Index

Back to Top

Jump to Model

Mathematical ToolBox

Jump to GXWeb

Descartes and his recognition of the importance of curvature set the path for many to follow, finding new connections and relationships right up until today. While Descartes allowed us to predict and calculate the radii of subsequent kissing circles, it took a trio of modern mathematicians in the 1990s to crack the secret of calculating and predicting, not just the sizes of all those kissing circles, but also their locations. It took the application of complex numbers to the problem to compute the centres of all those circles! Perhaps most amazingly, it turned out to be Descartes' Kissing Circle Theorem once again which lay at the heart of this solution! Take a moment or two to study the image of the bug-eye gasket shown here, and the steps which follow, laying out the solution to the problem of finding both curvature and centre of subsequent kissing circles. (With grateful thanks to Dana McKenzie for an enlightened and very enjoyable discussion of this topic!)

Hide ⇑

 

---

 

Show

Seeking Your Centre

Index

Back to Top

Jump to Model

Mathematical ToolBox

Jump to GXWeb

As we have seen in our exploration of Descartes and his Kissing Circles Theorem, if four circles have curvature a, b, c and x - and hence radii \(\frac{1}{a}, \frac{1}{b}, \frac{1}{c}\)and \(\frac{1}{x}\) - then \[(a+b+c+x)^2 \]\[= 2\cdot (a^2 + b^2 + c^2 + x^2)\] Solving for x gives two solutions for the curvature of the fourth circle: \[x = a + b + c \]\[\pm\]\[2\cdot\sqrt{(a\cdot b + a\cdot c + b\cdot c)}\]

Initial Curvatures: [-1, 2, 2, 3] ⇑ Tap for more gaskets...

As the figure in the previous section shows, Descartes' formula greatly simplifies the task of finding the size of the fourth circle, assuming the sizes of the first three are known.

It is much less obvious that the very same equation can be used to compute the location of the fourth circle as well, and thus completely solve the drawing problem. This fact was discovered in the late 1990s by Allan Wilks and Colin Mallows of AT&T Labs, and Wilks used it to write a very efficient computer program for plotting Apollonian gaskets. Descartes himself could not have discovered this procedure, because it involves treating the coordinates of the circle centers as complex numbers. Imaginary and complex numbers were not widely accepted by mathematicians until a century and a half after Descartes died. In 2001, when Wilks, Mallows and Jeff Lagarias published a long article in the American Mathematical Monthly, they ended it with a continuation of Soddy's poem entitled The Complex Kiss Precise: Yet more is true: if all four discs Are sited in the complex plane, Then centers over radii Obey the self-same rule again. The secret which eluded so many before lay in thinking of the centres of each of our kissing circles as \(x+i\cdot y\) instead of the cartesian form of \((x, y)\). Applying Descartes' Theorem then involves the product of three such centres (say \(x_a+i\cdot y_a, x_b+i\cdot y_b\) and \(x_c+i\cdot y_c\)) with their corresponding curvatures a, b and c.

If we let \(X = x + i\cdot y\) and \[A = a \cdot (x_a+i\cdot y_a)\] \[B = b \cdot (x_b+i\cdot y_b)\] \[C = c \cdot (x_c+i\cdot y_c)\] then \[(A+B+C+X)^2 \]\[= 2\cdot (A^2 + B^2 + C^2 + X^2)\] Solving for x gives two solutions: \[X = A + B + C \]\[\pm\]\[2\cdot\sqrt{(A\cdot B + A\cdot C + B\cdot C)}\] Dividing each by the curvature of the fourth circle where d1 and d2 are the solutions for the usual curvature quadratic: \[d = a + b + c \]\[\pm\]\[2\cdot\sqrt{(a\cdot b + a\cdot c + b\cdot c)}\] Then centres of the fourth circle are: \[x + i\cdot y = X/d1,\]\[x - i\cdot y = X/d2\] Example 1: [-1,2,2] Example 2: [2,2,3]

Hide ⇑

 

---

---

 

Drag circle centre P and use the Radius(P)-slider below to measure the radii of different circles.

Test Yourself!

This document requires an HTML5-compliant browser. Gasket Depth ▶ 1 30 500 Radius(P) ▶ 0 0.1 1 Descartes Configuration ▶ 0 0 48 App generated by GXWeb

Initial Triplets ([\(k,x\cdot k, y\cdot k)\) : [-1, 0, 0] [2, 1, 0] [2, -1, 0] [3, 0, 2] Show/Hide Curvatures Show/Hide Fill Center(P): P(x) : P(y) : Center(30): (0.07, 0.28); Radius(30): 0.00935 Curvature(30): 107 Set P Circle (use Gasket Depth)

RESET

Index

Back to Top

Jump to GXWeb

---

 

Show

Apollonian Gasket Spreadsheet Explorer

This browser-based spreadsheet uses the handsontable JavaScript library.

 

Hide Current
Coordinates Show Integral
Configurations Hide Integral
Curvatures

 

Hide Current
Coordinates Show Integral
Configurations Hide Integral
Curvatures

Hide ⇑

Index

Back to Top

Jump to Model

Jump to GXWeb

 

---

---

 

Show

Mathematical ToolBox

Index

Back to Top

The Challenges

Jump to Model

Explore Further

Jump to GXWeb

Input \[f(x)\] \[g(x)\] \[h(x)\]

RESET ToolBox CAS Toolkit   Select a CAS Tool... CAS Evaluate Solve Derivative Integral Tangent Normal CAS Toolkit help... CAS Evaluate Solve Derivative Integral Tangent Normal Reference: Nerdamer Symbolic JavaScript Use the CAS Evaluate option from the dropdown menu above to solve an expression or equation in the \(f(x)\) MathBox. Click on the following to try: Solve(x^2=x+1,x) Solve(x^2=x+1,x),x Notice the difference between these two results? Adding an extra \(,x\) at the end forces an \(exact\) rather than a \(numeric\) result! And some more to try (just click on each line): pFactor(320) (Prime factors) sqcomp(x^2-4*x+3,x),x (Complete the Square) nthroot(10,3) (Enter into the MathBox as \ nthroot [space] 3 [space] 10 [space]) Reset CAS help Use the Solve option from the dropdown menu above to solve an expression or equation in the \(f(x)\) MathBox, or enter solve(an equation) in \(f(x), g(x)\) or \(h(x)\). Reset CAS help Use the Derivative option from the dropdown menu above to differentiate a function in the \(f(x)\) MathBox, or enter \(d/dx\)(a function) in \(f(x), g(x)\) or \(h(x)\). Reset CAS help Use the Integral option from the dropdown menu above to integrate a function in the \(f(x)\) MathBox, or enter \(int\)(a function) in \(f(x)\). For definite integrals, perform the integration as described using the dropdown, and enter end values when requested. Try \(\int(x^2-x-1,0,x)\) for example. Use the \(x\) box or slider to vary this. View example Reset CAS help Display the tangent (or Normal) of \(f(x)\) for the current value of \(x\) using the Tangent/Normal button, or enter tangent (or tngnt) or normal directly into the graph mathBoxes - set the desired x-value first. View example Reset CAS help

---

Continued Fraction Timing: Key Signature: Switch Views: notes <=> frequencies About   Continued fractions are awesome. Every real number, rational and irrational, can be represented by a continued fraction - the rational ones are finite, of course, but both finite and infinite offer some wonderful patterns and opportunities to explore! Use the MathBox above to enter a value to express as a continued fraction. For example, try \(37 \over 15\), \(\pi\), \(\phi\) or even \(\frac{225}{157}\). Would you like to explore them further?

Function Table About   Use the Table button to display function table values for \(f(x), g(x)\) or \(h(x)\). For example, try \(x^2-x-1\) and \(\frac{d}{dx}(x^2-x-1)\).

 

---

---

 

Show

WolframAlpha: CAS+

Index

Back to Top

Jump to Model

The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!

Submit Build your own widget »Browse widget gallery »Learn more »Report a problem »Powered by Wolfram|Alpha Terms of use Share a link to this widget: More Embed this widget »

 

---

---

 

Show

Construct your own Model with GXWeb

Index

Back to Top

Jump to Model

---

Tap here to see how easily you can
create your own gasket with GXWeb

Hide GXWeb

 

---

---

 

Show

Behind the Scenes

Index

Back to Top

Jump to Model

 

Learn How: Create your own GXWeb Assessment Task

Learn How 2: Take GXWeb to the Next Level

View JavaScript Task Code (gasketgx.js)

View JavaScript GXWeb Code (gxgasket.js)

View JavaScript Shared Code (sharedcodend.js)

Index

Back to Top

Jump to Model

---

---

 

©2021 Compass Learning Technologies ← Live Mathematics on the Web ← Geometry Expressions Showcase ← GXWeb Apollonian Gaskets and Mathematical Bubbles