©2021 Compass Learning Technologies ← GXWeb Showcase ← GXWeb Concrete Algebra ← New Questions

Courses | Software | Readings | Links Good Software | Strategic Software Use | Mathematics Learning Culture | New Questions | Challenge and Support | Comments?
© 1996: The University of Newcastle: Faculty of Education
Some problems...
Take a moment to look closely at a recent examination paper. How many of the questions and tasks are effectively made trivial by new mathematical technology?
A significant aspect of learning to use these new tools remains learning to ask new questions.
Here are a few interesting ones I have found over the past few years. For a deeper consideration of these issues, you might then like to read the paper, Challenge and Support, which was written for the Graduate course, EDGS646, Teaching mathematics from a problem posing and problem solving approach (Faculty of Education, University of Newcastle).
- Simplify
(Simon, 1992, p. 702)
- The sum of two numbers is 28. The product of the numbers is 7. Find the sum of the reciprocals of the numbers. (NCTM, 1988, p. 68)
- Find all real values of x that satisfy
Are you sure you have them all? (NCTM, 1988, p. 19) 
- Find x2 if x satisfies the equation
(NCTM, 1988, p. 90)
- Solve |x - 1| + |x + 4| <= 6 (NCTM, 1988, p. 213)
- Solve
(NCTM, 1988, p. 169)
...and some explorations
- How many functions can you find which are their own inverses? How does a function affect its own inverse?
Describe the domains and ranges of sin(arcsin(x)) and acrsin(sin(x)).
- How many functions can you find such that
f(x) + k = f(x + k), for constant k?
- How do you define a perfect square?
Is 2x2 + 4x + 2 a perfect square? Why or why not?
In how many different ways can a perfect square be defined?
- A popular method for solving equations involving absolute value is to square both sides. Explain why this method works. Will it always work?
In how many different ways can you solve
|| x | - 2| = 1 ?
- The points A(-1, 1), B(1, 3), C(3, 1) and D(1, -1) form a quadrilateral. In how many different ways can you prove that the quadrilateral is a rhombus?
- Think of a number. Double it. Subtract 8. Divide your result by 2 and add 4. You should have the same number you started with. Why?
Think of a number. Add 11. Multiply by 3. Subtract 15. Now subtract twice the number you began with and take away 18 from the result. Are you back where you began? Why?
Now make up a few of your own "Think of a number" games.
- If you are told that a function ø(x) has ø'(2) = 0 and ø"(2) > 0, what can you deduce about ø(2)?
- If x = 2 and x - 2 = 0 are identical mathematical statements, then why does squaring one produce an equation with two distinct real solutions, while squaring the other produces an equation with only one?
Now solve the equation
- Study the graph of the composite function sin(tan(x)). What is happening at each of the fuzzy bits? If the function is periodic, then why do each of these appear different?
Now study the graph of the composite function F(x) = cos(arcsin(x)).
Is it really a semicircle, or does it just resemble one. How might you prove this?
- Define a function R as follows:
R(x) = R(x + 2) for all x
R(x) = x + 1 for 0 <= x < 2.
What do you understand by the statement R(x) = R(x + 2)? How would you explain this to someone else?
Can you describe the graph of y = R(x), and use it to find the value of R(4.5)? (Barnes, 1988)
- Suppose transportation specialists have determined that G(v), the number of litres of fuel per hundred kilometres that a vehicle consumes is a function of the speed of the vehicle, in kilometres per hour.
Interpret, in terms of fuel consumption, the finding that G'(110) = -0.4.
How might this fact be used in a debate about setting an appropriate national speed limit? (Heid, 1988)
- E(t) represents the number of people unemployed in a country t weeks after the election of a fiscally conservative Prime Minister.
Translate each of the following facts about the graph, y = E(t), into statements about the unemployment situation:
- The y-intercept of y = E(t) is 2 000 000
- E(20) = 3 000 000
- The slope of y = E(t) at t = 20 is 10 000
- E"(36) = -800 and E'(36) = 0 (adapted from Heid, 1988).
Mathematics learning culture

Good Software | Strategic Software Use | Mathematics Learning Culture | New Questions | Challenge and Support | Comments?
© 1996: The University of Newcastle: Faculty of Education
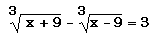
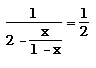

 Challenge and support
Challenge and support