©2020 Compass Learning Technologies → Live Mathematics on the Web → GXWeb Curve Construction Collection → GXWeb Cissoid of Diocles
GXWeb Cissoid of Diocles
Saltire Software, home of Geometry Expressions and GXWeb
GXWeb Curve Construction Collection (like this one!)
About the Cissoid (from Wolfram MathWorld)
The Cissoid of Diocles is a curve generated from two given curves (here a line and a circle) and a point O (the pole).
| \(a\) | |||||
| 0 | 0 | 5 | |||
| \(b\) | |||||
| 0 | 0 | 5 | |||
| \(\theta\) | |||||
| -6.283 | 0 | 6.283 | |||
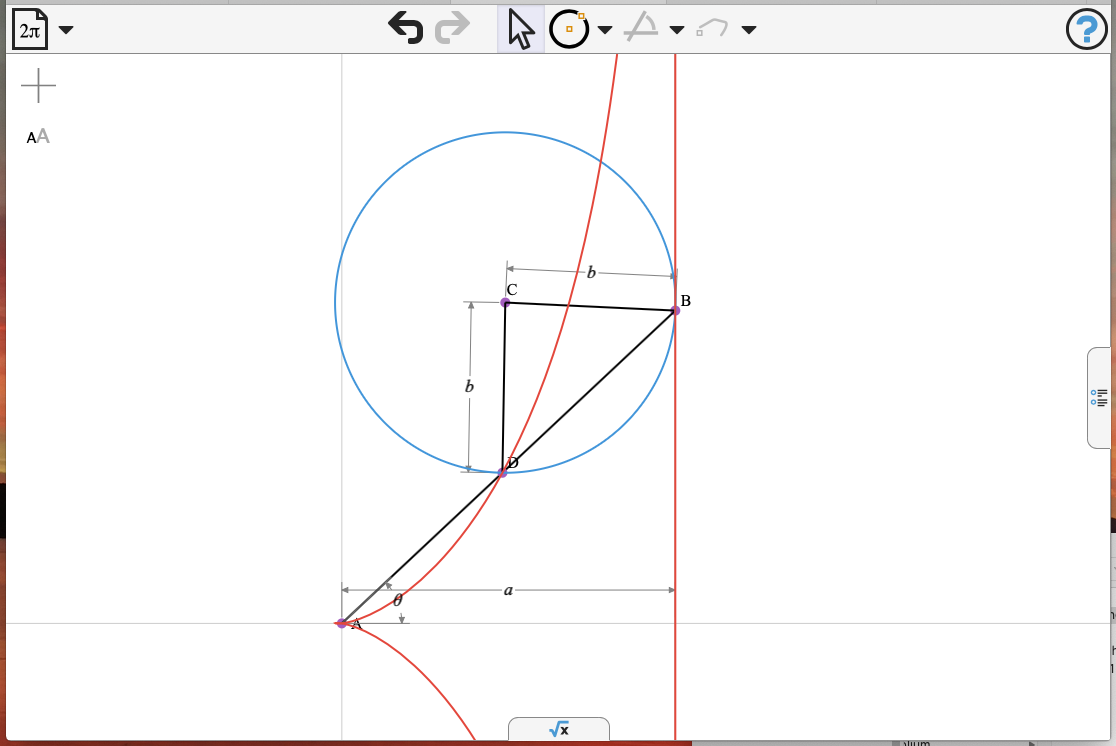 | Explore the model here and observe connections between the cissoid and the Strophoid. The Cissoid constructed here is the locus of point C where \(a = Length(OD)\) \(b = Length(AB) = Length(BC)\) and \(angle(AOD) = \theta\). |
Cartesian equation: \[X^3+X·Y^2+2·X^2·b-a·(X^2+Y^2)\]
Try this yourself with the tools below...
Construct your own Model with GXWeb
WolframAlpha: CAS+
The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!
Behind the Scenes
©2020 Compass Learning Technologies ← Live Mathematics on the Web ← GXWeb Curve Construction Collection ← GXWeb Cissoid of Diocles