Review of Complex Numbers

Complex Number Exercises

  1. (1993 Q2 c, e)

    (c) Find the equation, in Cartesian form, of the locus of the point z if

    (e) Let P, Q and R represent the complex numbers w1, w2and w3 respectively. What geometric properties characterise triangle PQR if

    Give reasons for your answer.

    2. Top of Page



  2. (1995 Q2d)

    The diagram shows a complex plane with origin O. The points P and Q represent arbitrary non-zero complex numbers z and w respectively. Thus the length of PQ is |z - w |.

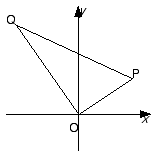    (i) Copy the diagram, and use it to show that

    (ii) Construct the point R representing z + w. What can be said about the quadrilateral OPRQ?

    (iii) If |z - w | = |z + w |, what can be said about the complex number ?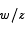

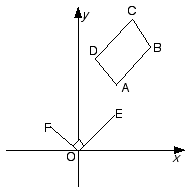    3. Top of Page



  3. (1991 Q2d)

    In the Argand diagram, ABCD is a square, and OE and OF are parallel and equal in length to AB and AD respectively. The vertices A and B correspond to the complex numbers w1 and w2 respectively.

    (i) Explain why the point E corresponds to w2 - w1.

    (ii) What complex number corresponds to the point F?

    (iii) What complex number corresponds to the vertex D?

    4. Top of Page



  4. z1 and z2 are two complex numbers such that

    (i) On an Argand diagram show vectors representing

    (ii) Show that

    (iii) If a is the angle between the vectors representing z1 and z2 show that

    (iv) Show that

    5. Top of Page



  5. On an Argand diagram the point A represents the real number 1, 0 is the origin, and the point P represents the complex number z which satisfies the condition

    (i) Show this information on a diagram and deduce that triangle OAP is isosceles.

    (ii) deduce that the locus of P is the union of a circle and part of a straight line, and show this locus on your diagram.

    (iii) Find z in mod-arg form if z also satisfies the condition

    6. Top of Page



  6. z1 and z2 are two complex numbers such that | z1 | = | z2 | and 0 < arg z1 < arg z2 < Pi/2. On an Argand diagram vectors OP and OQ represent z1 and z2 respectively. Angle QOP = Pi/3 and OPRQ is a parallelogram.

    (i) Draw a diagram to show this information.

    (ii) Find the value of

    (iii) Show that

    7. Top of Page



  7. If

    show that

    8. Top of Page



  8. Find the locus of z if

    is (i) purely imaginary.

    (ii) purely real.

    9. Top of Page



  9. If z is a point on the unit circle with arg z = a

    (i) prove that

    (ii) find the arguments of

    in terms of a.

    10. Top of Page



  10. (1970 Q9(iii))

    The four complex numbers 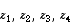are represented on the complex (Argand) plane by the points A, B, C, D respectively.

    determine the possible shape(s) for the quadrilateral ABCD.

    11. Top of Page



  11. E is the centre of a square ABCD lettered anticlockwise on the Argand diagram. E and A are the points -2 + i and 1 + 5i respectively.

    Find the complex numbers represented by the points B, C and D.



Top of Page

All care but no responsibility taken with these solutions. Comments, corrections and suggestions would all be most welcome: send to Stephen Arnold.

Back to Review of Complex Numbers