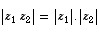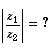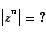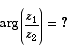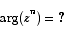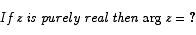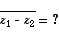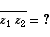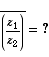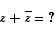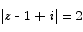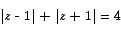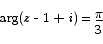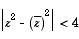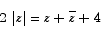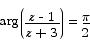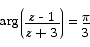Complex Numbers Review

1. Complex Numbers Made Easy
2. Properties of Mods and Args
3. Properties of Conjugates
4. Curves and Regions in the Argand Diagram
5. Interactive Complex Arguments
6. Representation of Complex Numbers by Vectors
7. Addition, Subtraction and Multiplication by Vectors
8. Some Review Questions

Properties of Mods and Args

Table of Contents

Properties of Conjugates

Table of Contents

Curves and Regions on the Argand Diagram

Table of Contents

You should instantly recognise the following:

You should be able to work out the following by putting z = x + i y in (or by using properties of mods, args, conjugates).

The following are worth knowing also (play with this interactive figure to help!):

Representation of Complex Numbers by Vectors

Table of Contents

We know that the complex number z = x + i y may be represented on the Argand diagram in one of two ways:

1. By the point Z with coordinates (x, y).
2. By ANY vector whose length equals |z | and whose direction is parallel to OZ.

NB: a complex number z is represented by the length and direction of a vector, and, if the vector begins at O, then its tip will actually be at the point that represents.z.

ADDITION, SUBTRACTION AND MULTIPLICATION BY VECTORS

Table of Contents

• ADDITION by drawing the diagonal of the parallelogram (or by completing the polygon).

• SUBTRACTION: the vector representing z₁ - z₂ is the vector from the point representing z₂ to the point representing z₁.

• MULTIPLICATION by a positive real number is represented by a scaling of the vector (with no change in direction).

• MULTIPLICATION by i: the vector representing i z is formed by the rotation of the vector representing z anticlockwise through 90º.

• MULTIPLICATION by a complex number: to multiply z by a complex number z₁ involves both a rotation through arg z₁ and a scaling by |z |.

Table of Contents

Back to My Home Page