©2019 Compass Learning Technologies ← Live Mathematics and STEM on the Web ← GXWeb Showcase ← A Search for Harmony and Other Perfect Problems
A Search for Harmony and Other Perfect Problems
Download supporting TI-Nspire™ documents for this page
What constitutes a "perfect problem"?
For me, it is one that spans the high school years, accessible for the young and less able in a genuine way, but challenging for seniors - something for everyone!
It CONNECTS the various branches of mathematics, and INTEGRATES Mathematics with other disciplines.
It must, of course, ENGAGE and cognitively EXTEND our students but, ideally, be relatively simple in expression.
Finally, it should give opportunities for creative expression. Not surprisingly, my favorite Perfect Problems are best explored using good technology.
Here, I share a few of those that I have stumbled across over the years, and invite you to begin your own collection!
A Search for Harmony
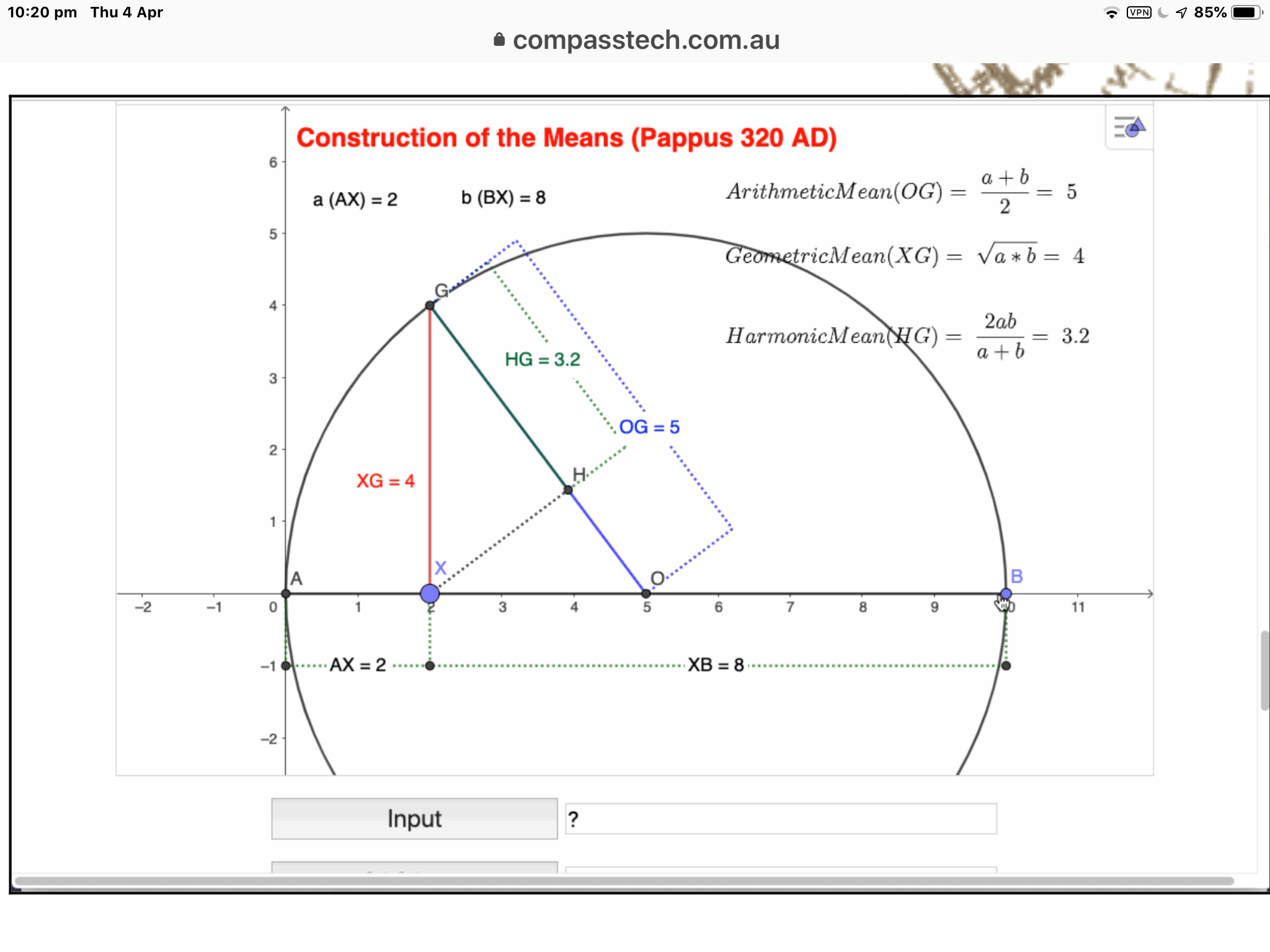
Many (many) years ago I became intrigued by a curious and (relatively) little known fellow called the harmonic mean. Although in schools these days we only hear about the arithmetic and geometric means, historically there were scattered references, all the way back to Pythagoras.
The harmonic mean seemed to appear in those annoying problems that just did not seem to behave the way we expect them to - they were counter-intuitive! This was a great indicator of something worthy of further investigation - anything that shakes our complacency (and that of our students) is a great place to start in engaging them.
So two questions began to drive my interest: what does the harmonic mean have to do with music? and what does the harmonic mean look like? (since the mathematics of the Greeks was largely visual and geometric, if they knew of this mean, then they knew how to construct it - but I could not easily find such a construction).
My search eventually led me literally to the bowels of the University of Sydney mathematics library and a very old book, where interesting discoveries awaited!
Click for TI-Nspire document
What is the "harmonic mean"?
How is it related to its more famous cousins?
What does it have to do with music?
To the Greeks, mathematics was largely visual - so how might Pythagoras have constructed the Harmonic Mean?
Is it of any practical use today?
Tap for more...
When teaching this activity, I would have students measure and listen to different scales using varying string lengths (or finger positions) on guitars (which are actually not as good for this purpose as instruments such as violins, which have no frets!).
I recently discovered that there are easily available tone generators for web browsers on any platform. What a great way to make this topic come to life!
For an extensive online exploration of this fascinating topic, visit Harmonic Mathematics
Areas and PaperFolding
The best lessons are those which involve physical engagement as well as cognitive engagement. This is one of my favourite lessons for classes at any level, from upper elementary/primary through to seniors and calculus.
The lesson always begins with folding and measuring paper, with an emphasis upon accuracy (equally important for those senior students, who often have not been asked to actually measure anything since they were in little school!)
Younger students could then aggregate their measurements to produce a scatter plot, clearly showing that there is a "best fold" which can then be estimated from the data and graph, with some discussion regarding why this might be the case.
Click for TI-Nspire document
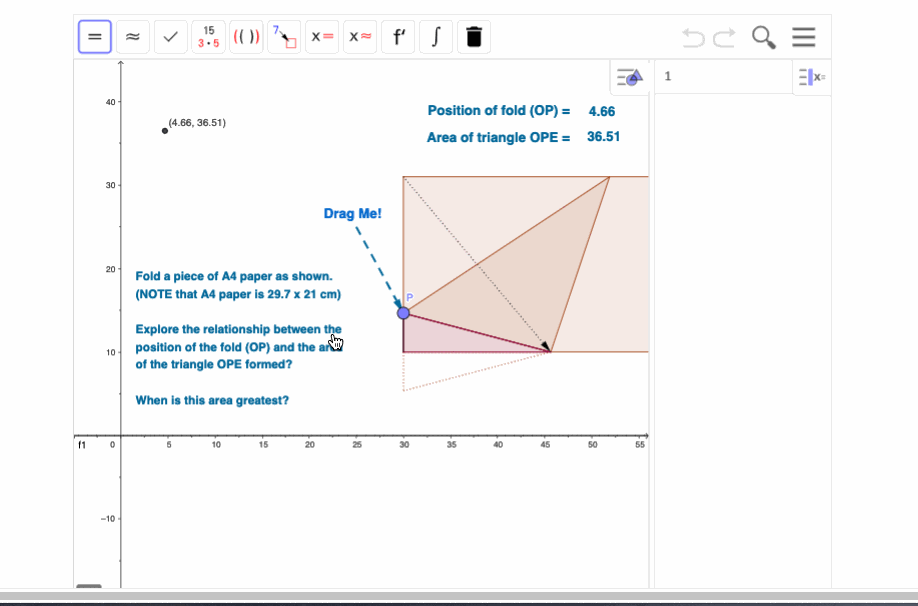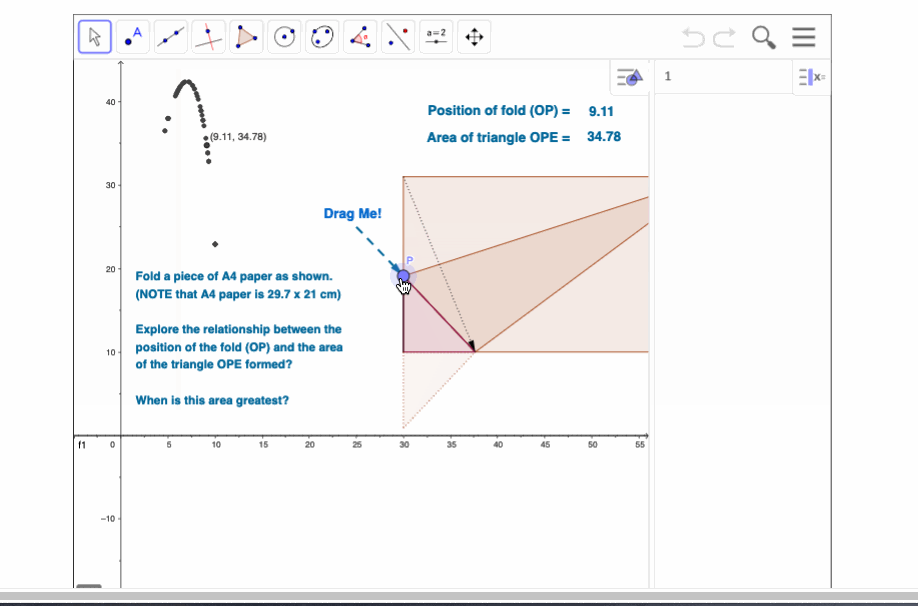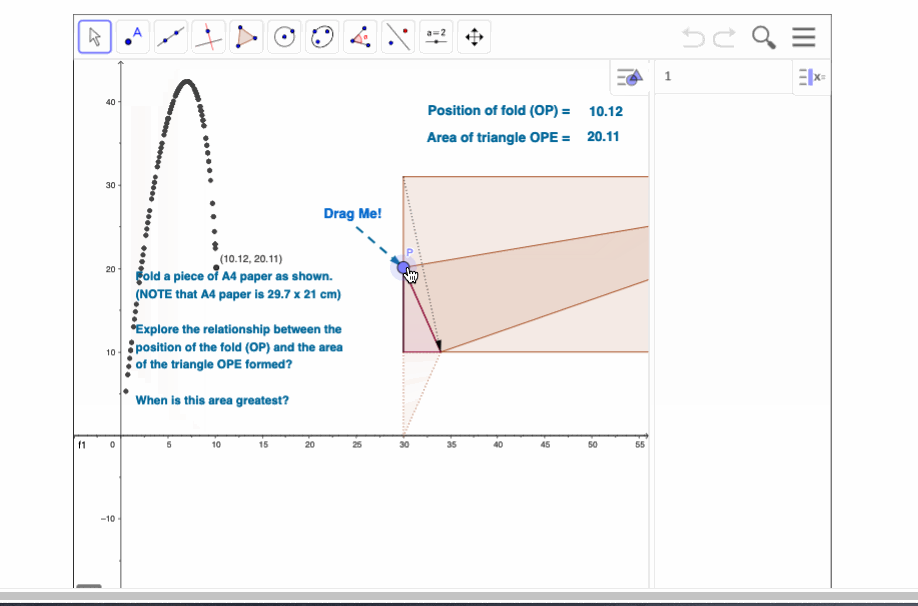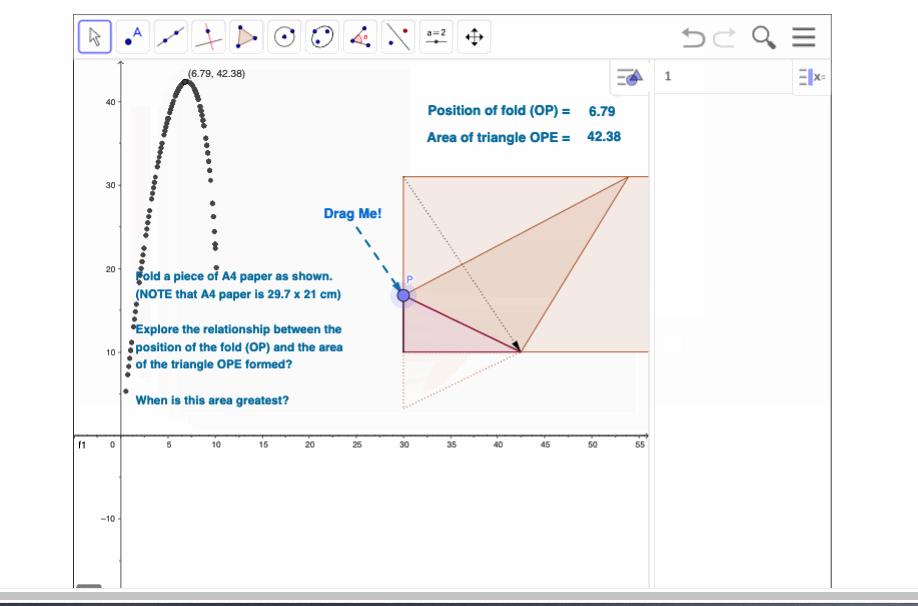
Turn a piece of paper to "landscape" mode (long side along top and bottom).
Now take the top left corner and fold it down to meet a point somewhere along the bottom (long) edge (as shown on the next page). This forms a triangle in the bottom left corner.
What fold gives the largest triangle? WHY?
Tap for more...
This marvellous hands-on activity ranges from data collection and measurement in the junior years, through functions and pythagoras, onto trigonometry and optimisation in the later years. There are interesting side trips that can be made - for example, suppose students collect measurements of base and hypotenuse and plot these - they will be introduced in a very practical way to linear functions! In fact, they will have a tangible example of negative gradient in the relationship between these two sides.
Note: Although A4 paper is used in this example, the activity is easily adapted to other sizes (such as US letter).
For an online exploration of this activity, visit Areas and PaperFolds onLine
String Art and Bezier Curves
Explore the creative side of mathematics with this string art explorer - create your own patterns, and then research the Bezier Curves that underly this.
This great exploration can culminate in an artistic product - produced using the geometric curves for younger students, or as a wonderful application of parametric functions for seniors. Young or old, there are opportunities for both creative expression and some deep mathematics.
Click for TI-Nspire document
Many of the lines you see on a computer - whether it is the letters you type in your word processor, or the lines that form the many designs and images that are found on the web - are created using a mathematical function called a bezier curve.
In this project, you will learn how to create these curves geometrically and algebraically and design your own patterns using these.
Tap for more...
For an online exploration of this activity, visit Bezier Curves onLine
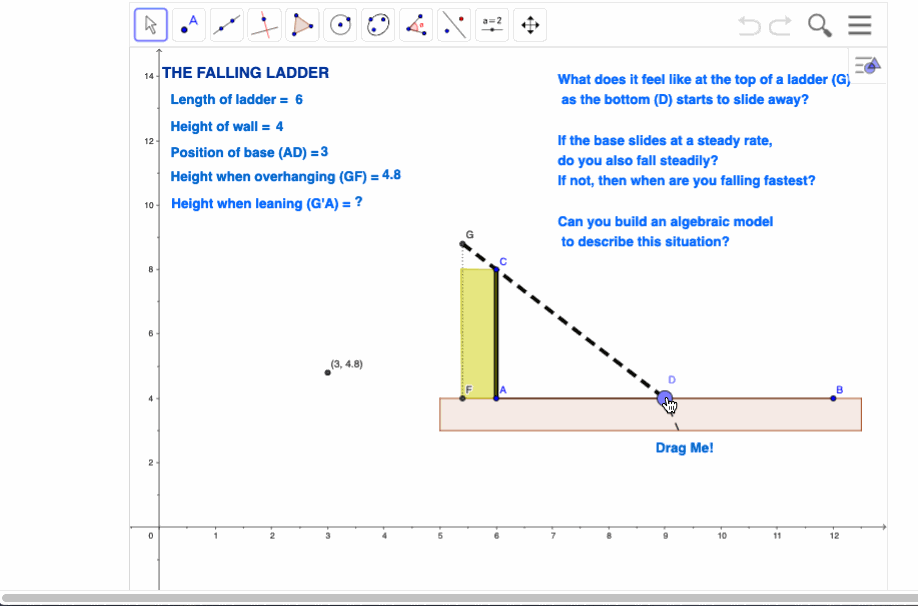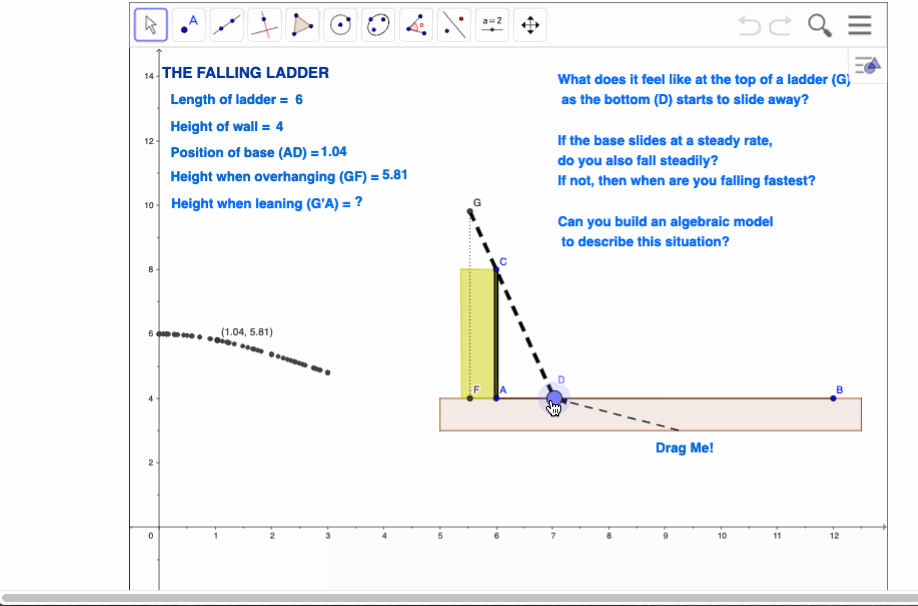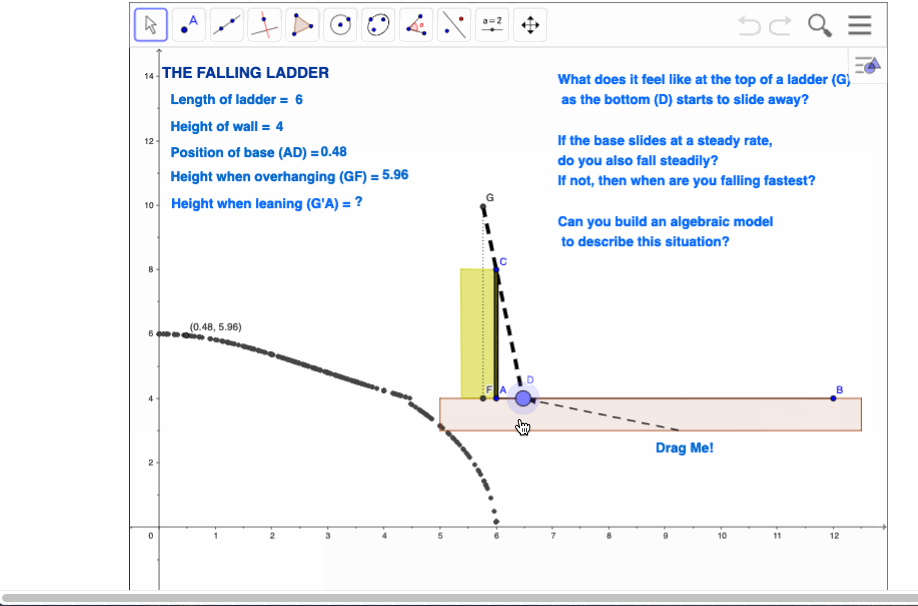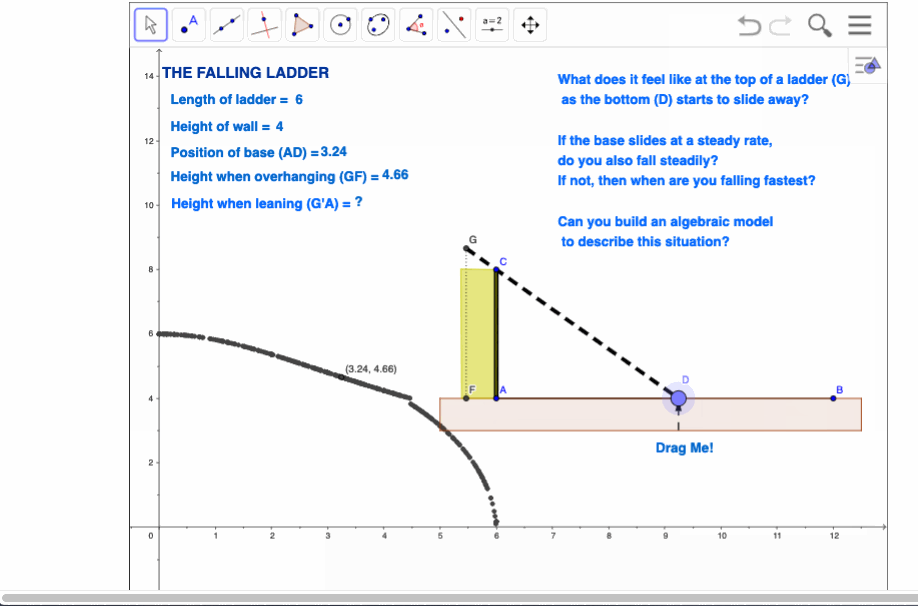
The Falling Ladder
This one has been done many times, and in many different ways.
The approach I have adopted here is to consider two scenarios - the ladder leaning against the wall, and the case where the top of the ladder overhangs the wall. Motion is quite different in each case, not surprisingly - and for those of us who have had the opportunity to experience this in reality, it is readily verified!
The chance to branch on to side paths is present throughout this activity. The primary focus is upon capturing the height of the top of the ladder above the ground, but in the case of the overhanging ladder, perhaps even more interesting is the path of the motion of the top of the ladder - once again, the result tends to catch the student by surprise and sends them back to think and play some more - always a good thing! At the end, they are challenged to consider the general case - what if the wall is not perpendicular to the ground?
Click for TI-Nspire document
What does it feel like at the top of a ladder as the bottom begins to slide away?
If the bottom slides away at a steady rate, do you also fall steadily?
If not, then what is the nature of your motion, and when do you fall fastest?
Tap for more...
Opportunities presented in this activity for me centre particularly upon students using a motion detector to actually conduct their own experiments, guiding and validating their conjectures. Not essential, but well worth any inconvenience involved.
The other key element (which is common to all of these activities for me) is the use of real language for the naming and defining of variables and functions. This is a critical and often overlooked advantage that good technology offers for the learning of algebra at all levels.
For an online exploration of this activity, visit The Falling Ladder onLine
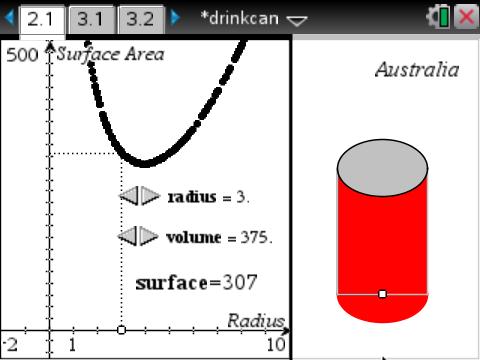
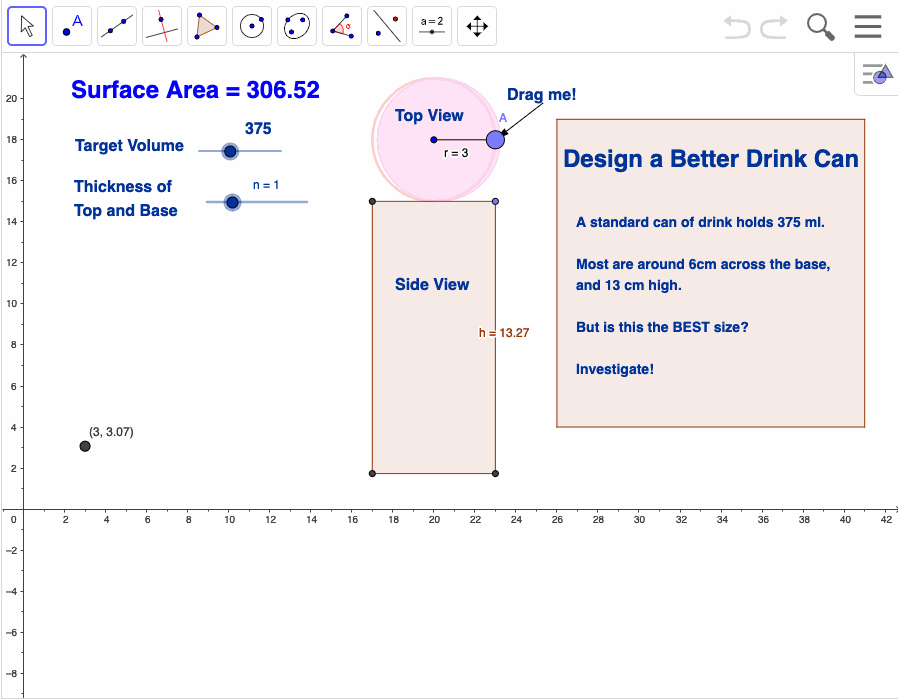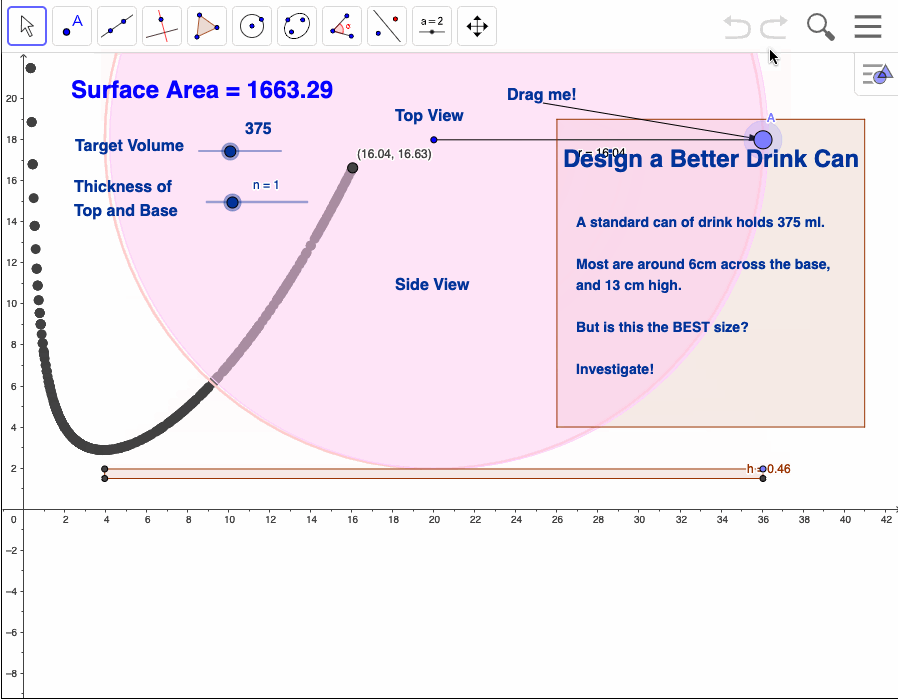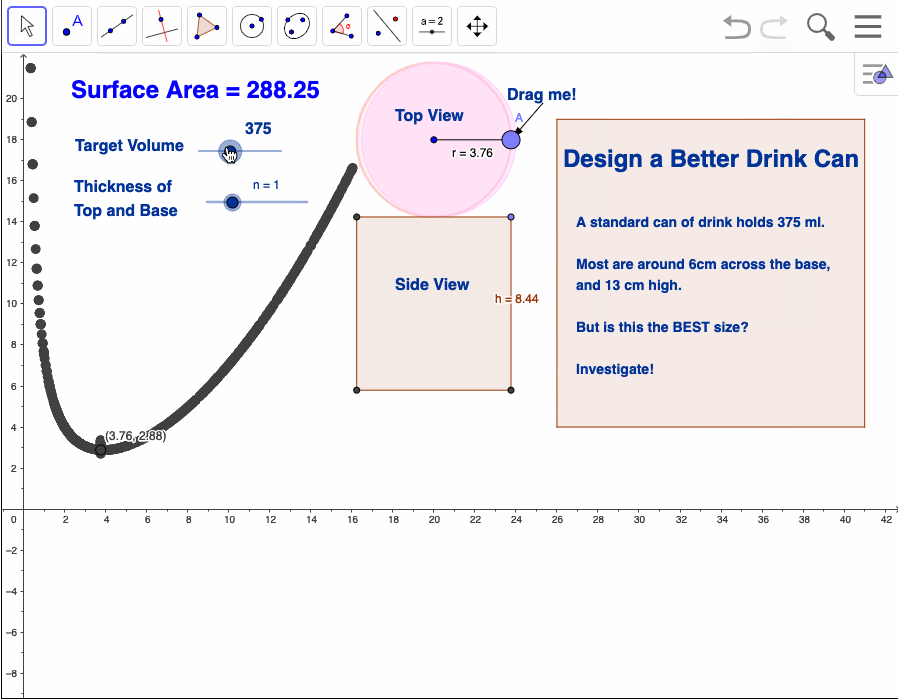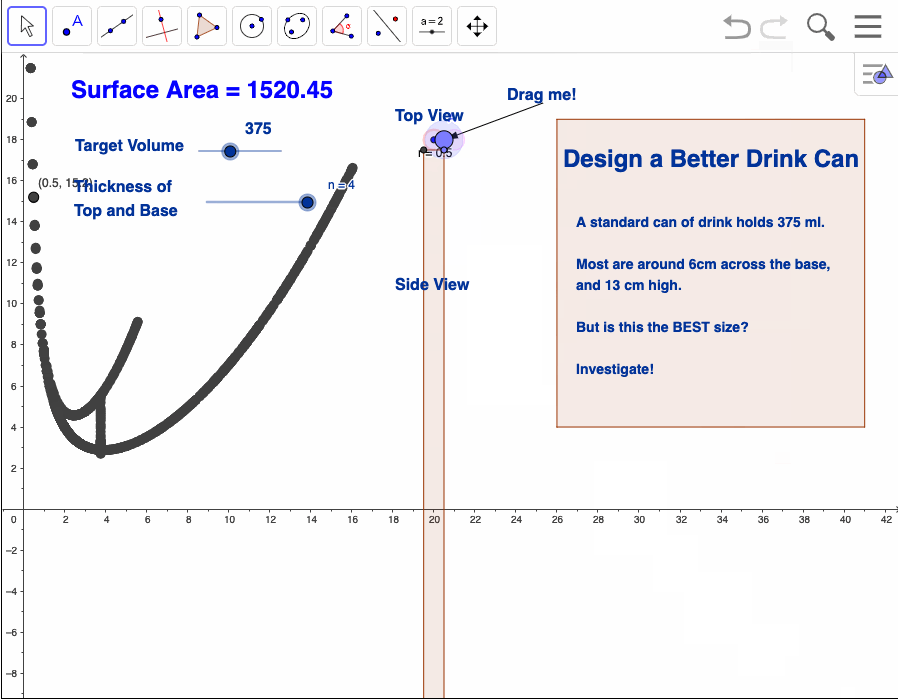
Design a Better Soft Drink Can
Most of my selection of "perfect problems" might be seen to fall into a class of algebraic modelling activities, and this is correct, but not the whole story. For me, the power of these projects is that they offer legitimate and worthwhile mathematical exploration for much younger and perhaps less able students. All are grounded in practical scenarios and afford opportunities for measurement, data collection and display, and interpretation of results.
This activity is a nice example of the sort of question that has, as its initial answer - "It depends." In this case - what are the best dimensions for a can of drink: well, it depends. Is a bath better or a shower? It depends. MacDonalds or KFC? You get the idea...
Click for TI-Nspire document
In Australia, a standard can of drink holds 375 ml. Most measure around 6cm across the base, and 13 cm in height.
In the United States, the standard 12 oz (355 ml) can measures 2.5 inches by 4.75 inches.
But are these the BEST sizes?
Tap for more...
Send them out to raid the cupboards at home for this one! Have them measuring anything they can lay their hands on that presents in a cylindrical container.
And spend a lot of time talking about the assumptions we make when we apply mathematics to real world problems.
For an online exploration of this activity, visit Design a Better Soft Drink Can onLine
For more great problems: and the
Home ← Live Mathematics and STEM on the Web ← GXWeb Showcase ← A Search for Harmony and Other Perfect Problems