©2020 Compass Learning Technologies → Live Mathematics on the Web → GXWeb Curve Construction Collection → GXWeb Hyperbola
GXWeb Hyperbola
Saltire Software, home of Geometry Expressions and GXWeb
GXWeb Curve Construction Collection (like this one!)
About the Hyperbola (from Wolfram MathWorld)
The Hyperbola is a plane curve for which the difference of the distances from two fixed points (the foci A and D) separated by a distance \(2\cdot f\) is a positive constant.
The ellipse and the hyperbola are closely related conics - can you see the values for a and f in this model for which it switches from hyperbola to ellipse and back again? Use the model to explore and study the cartesian equation below.
| \(a\) | |||||
| 0 | 1 | 10 | |||
| \(f\) | |||||
| 0 | 0 | 10 | |||
| \(\theta\) | |||||
| 0 | 0 | 1.57 | |||
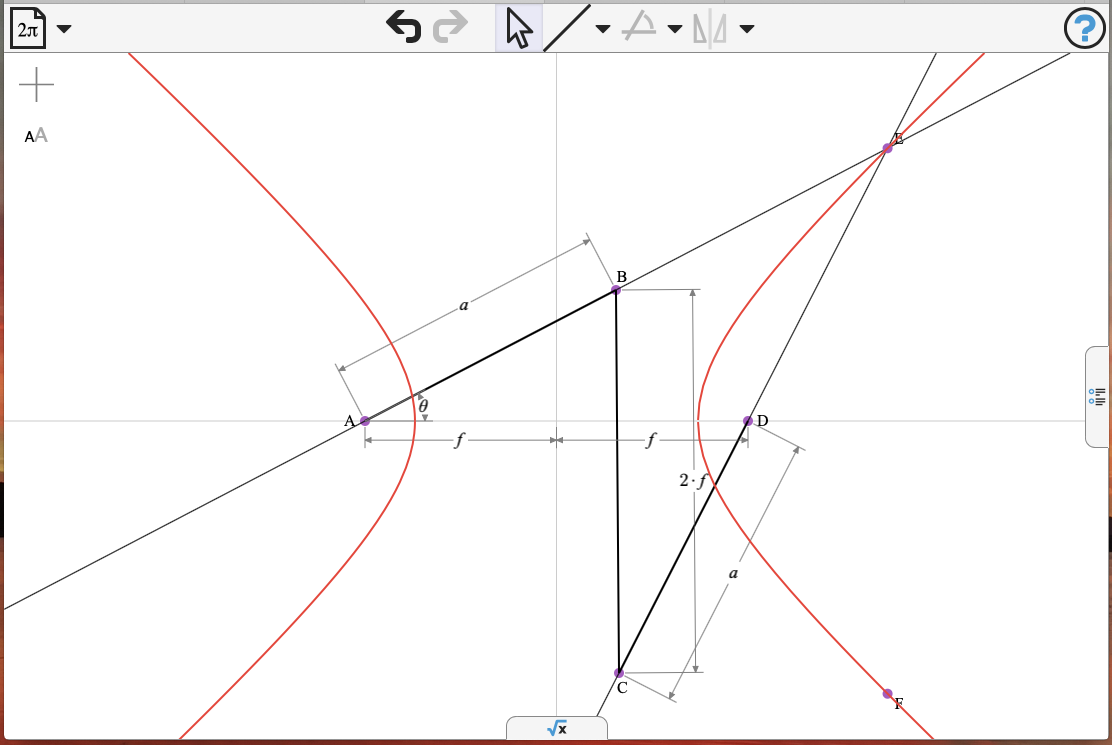 | The Hyperbola constructed here is the locus of points E and F where \(a = Length(AB) = Length(CD)\) \(2*f = Length(AD) = Length(BC)\) and \(angle(BAD) = \theta\). |
Cartesian equation: \[4·Y^2·a^2-a^4+4·a^2·f^2+X^2·(4·a^2-16·f^2)\]
Try this yourself with the tools below...
Construct your own Model with GXWeb
WolframAlpha: CAS+
The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!
Behind the Scenes
©2020 Compass Learning Technologies ← Live Mathematics on the Web ← GXWeb Curve Construction Collection ← GXWeb Hyperbola