©2020 Compass Learning Technologies → Live Mathematics on the Web → GXWeb Curve Construction Collection → GXWeb Folium of Descartes
GXWeb Folium of Descartes
Saltire Software, home of Geometry Expressions and GXWeb
GXWeb Curve Construction Collection (like this one!)
About the Cardioid (from Wolfram MathWorld)
The Folium of Descartes is an algebraic curve defined by the equation \(X^3+Y^3-X·Y·a\). It forms a loop in the first quadrant with a double point at the origin and asymptote \(x+y+a=0\). It is symmetrical about \(y=x\). The name comes from the Latin word folium which means "leaf".
The curve was first proposed by Descartes in 1638. Its claim to fame lies in an incident in the development of calculus. Descartes challenged Fermat to find the tangent line to the curve at an arbitrary point since Fermat had recently discovered a method for finding tangent lines. Fermat solved the problem easily, something Descartes was unable to do. Since the invention of calculus, the slope of the tangent line can be found easily using implicit differentiation.
| \(a\) | |||||
| 0 | 0 | 10 | |||
| \(\theta\) | |||||
| -1.57 | 0 | 1.57 | |||
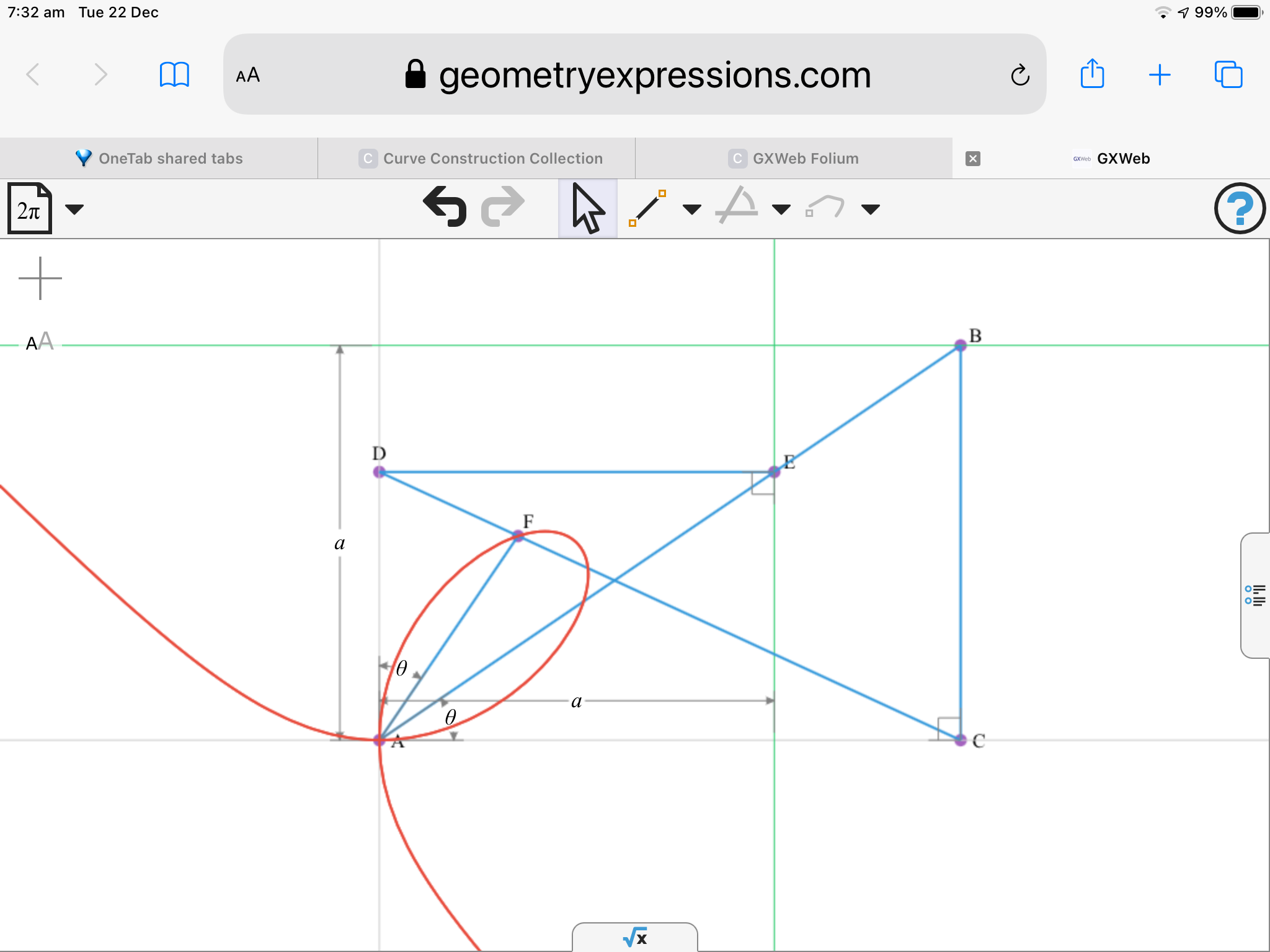 | The Folium of Descartes constructed here is the locus of point E where \(a = Length(OF) = Length(OG)\) and \(angle(AOB) = \theta\). |
Cartesian Equation: \[X^3+Y^3-X·Y·a\]
Try this yourself with the tools below...
Construct your own Model with GXWeb
WolframAlpha: CAS+
The powerful Wolfram Alpha online CAS engine will answer almost anything you care to ask - within reason! From the continued fraction of pi to Solve x^2=x+1 to the population of Australia!
Behind the Scenes
©2020 Compass Learning Technologies ← Live Mathematics on the Web ← GXWeb Curve Construction Collection ← GXWeb Folium of Descartes