©2020 Compass Learning Technologies ← Live Mathematics on the Web ← Algebra Explorer ← Farey Sequences and Ford Circles
Farey Sequences and Ford Circles
With thanks to Dan McKinnon: Please see the blog post here.
Suppose you wanted to make a list of all the rational numbers between 0 and 1. How would you start?
One approach might be to begin with the denominators of the fractions: first, list those with denominator 1 - zero and 1: \(\frac{0}{1}, \frac{1}{1} \).
Next, add those with denominator 2: \(\frac{0}{1}, \frac{1}{2}, \frac{1}{1} \).
Add those with denominator 3 ( \(\frac{0}{1}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{1}{1} \)) and you are on your way to the Farey Sequence! This last would be referred to as the Farey Sequence of Order 3.
So many patterns! So much to explore...
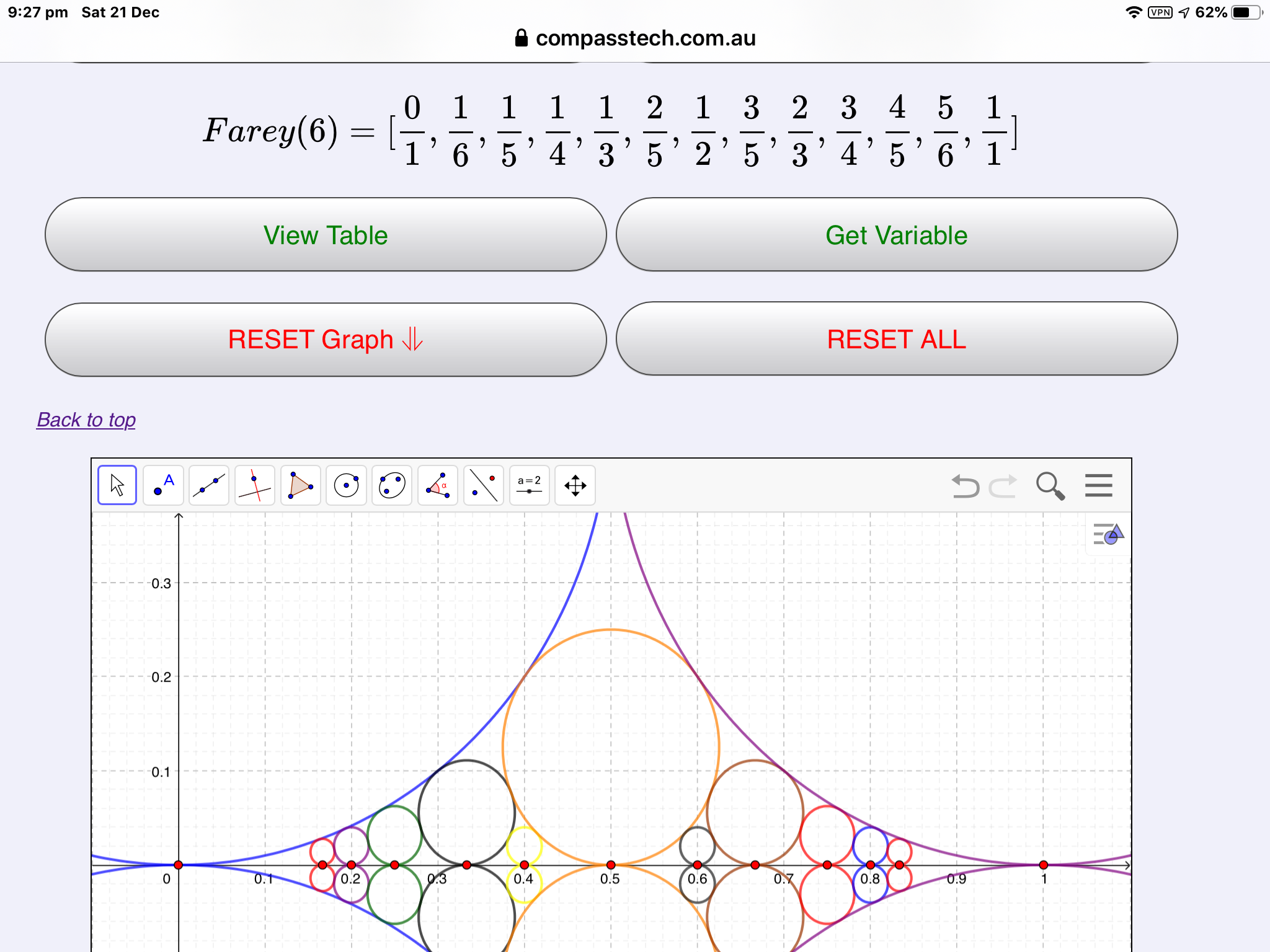
Plot these Farey numbers on the number line: for each \(\frac{a}{b}\) draw a circle of radius \(\frac{1}{2b^2}\) and centre \(\left(\frac{a}{b},\frac{1}{2b^2}\right)\). These are the Ford Circles!
AND... If you plot the numerators against the denominators of a Farey Sequence, then you get the amazing Farey Starburst: Try fareyStar(n) (or just star(n)!)
Exploration 1: Suppose you wanted to know the next term of the sequence between two values, \(\frac{a}{b}\) and \(\frac{c}{d}\)?
Easy! Just add the numerators and the denominators! \(\frac{a+c}{b+d}\). The resulting fraction is called the mediant of \(\frac{a}{b}\) and \(\frac{c}{d}\).
Be warned, though, that this term may not appear in the next sequence, or even the one after that...
Exploration 2: What do you notice when you cross-multiply numerators and denominators of pairs of Farey neighbours? (If \(\frac{a}{b}\) and \(\frac{c}{d} \)are consecutive terms of a Farey Sequence, consider \(b*c\) and \(a*d\)...)
Exploration 3: Just for interest... you might consider the count of each Farey Sequence.
How many terms make up the Farey Sequence of Order 1, Farey(1)? Order 2, Farey(2)? Order 3, Farey(3)? etc. Use fareyCount(n) (or just fcount).
Can you see a pattern? (But be careful... first impressions might prove deceiving!)
Exploration 4: And finally, what do you notice about the continued fractions of \(\frac{\sqrt{5}+2n-1}{2}\)? (These are called Noble Numbers).
Some more interesting Noble Numbers may be formed using tau (\(\tau: \frac{1}{\phi}\)), the reciprocal of phi (\(\phi\)), the Golden Ratio: For example, \(\frac{\tau}{1+3\tau}\), but what about \(\frac{2+5\tau}{5+12\tau}\)?
To better understand the continued fractions of Noble (and even Near-Noble Numbers) you may need to delve a little further into Farey Sequences and Ford Circles! In terms of Noble Numbers, you might note that 0 and 1/3 are Farey neighbours in Farey(3), while 2/5 and 5/12 live next door to each other in Farey(12).
Peek behind the scenes...