©2009 Compass Learning Technologies ← Mathematical Software: MANSW 2009
What's New in Mathematics Software 2009?
MANSW 2009
Steve Arnold (steve@compasstech.com.au)
As New South Wales moves ahead of all other Australian states and territories in their adoption of netbooks for schools, the choice of appropriate software for the teaching and learning of mathematics becomes ever more important. As always, we are spoiled for choice - there are many great software packages available, both free and commercial, and the issue becomes the selection of tools that will best suit the needs of teachers and students in our schools.
This year, there are three packages that stand out for me: Math Illustrations (from Saltire Software, the makers of the outstanding Geometry Expressions), MathRider (by Ted Kosan, an free and open source package which brings together a collection of powerful mathematical tools - including the ever-popular GeoGebra - in one envelope), and TI-Nspire (from Texas Instruments, which continues to just get better and better as the most complete mathematical software solution available for schools).
The mathematical vehicle which I will use to introduce these software tools represents a nice integration of algebra and geometry, appropriate since all these tools offer support for such integration.
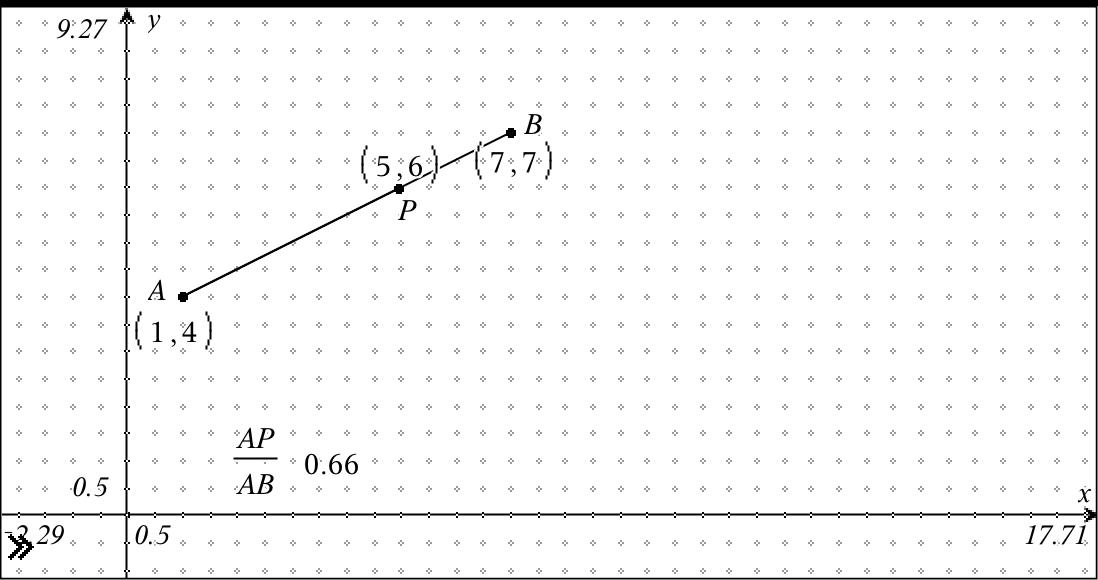
We are all familiar with the midpoint formula, and many of us have encountered its more generalised form in teaching the Mathematics Extension 1 course (and its earlier incarnations).
In the example shown, we wish to divide the interval between points (1,4) and (7,7) in the ration 2:1, giving us the resultant point (5,6).
Maybe it was just me, but I have always found the generalised form to be unnecessarily complicated and confusing for students, and would generally recommend a much simpler approach. Consider the following:
Study the formula given above: consider what happens when the value of the parameter "r" is 0? When it has value 1? It is easily seen that this is an algebraic representation of the geometric idea of a "slider" point which varies between two endpoint values.
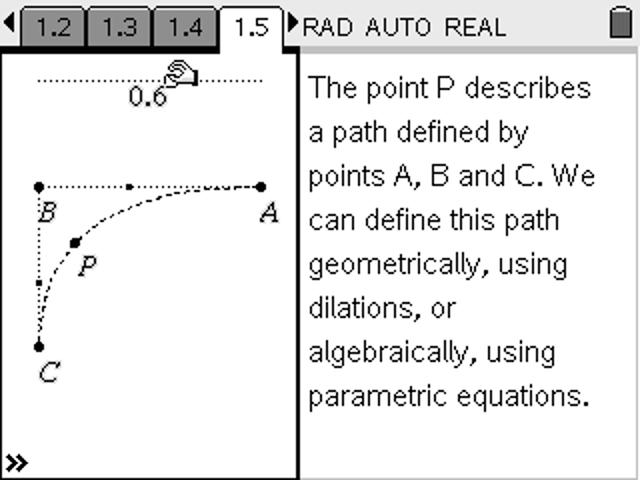
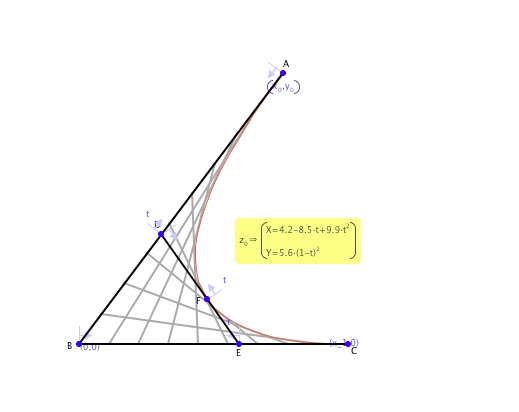
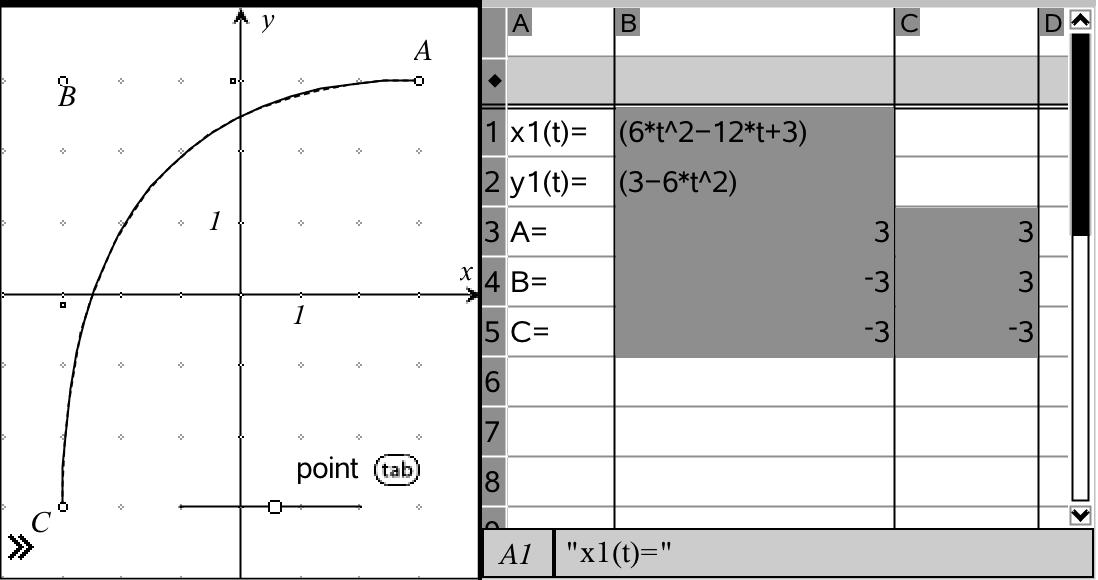
It is easy to see how this works with a point placed proportionately between two other points. But what happens if we have a third point, C, and we are after a point proportionately positioned in relation to all three points?
Algebraically, this is defined by a neat recursive function, as shown.
Geometrically, if we take dilations between 3 points, we get a curve which is called a quadratic bezier curve.
Let's see how our three featured software packages handle this little interplay between algebra and geometry!
Top of Page
Math Illustrations (like its big algebraic brother,
Geometry Expressions) offers a constraint-based dynamic geometry environment which is ideal for creating beautiful annotated mathematical figures and diagrams, while at the same time making it very easy to explore geometric constructions.
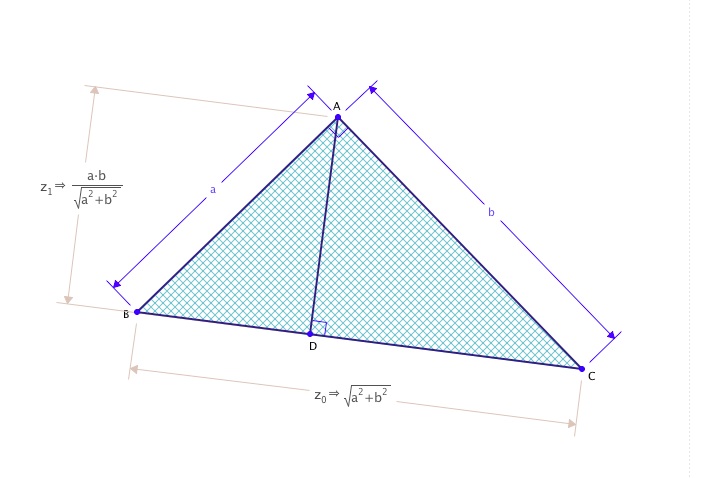
For those who have not experienced Geometry Expressions, imagine going from a general triangle to the following in just half a dozen steps!
Geometry Expressions combines a constraint-based geometry system with a powerful computer algebra engine which allows it to work, not just with real measurements but with symbolic forms as well.
Math Illustrations removes the computer algebra part but leaves a very capable geometry tool which automatically annotates and displays guidelines to present mathematical diagrams very clearly and very easily. This should be in every teachers' toolkit!
Even without the CAS engine, this is a very useful and well presented package which offers plenty of opportunity for geometric exploration on the part of students, and an easy and effective way for teachers to create effective illustrations for worksheets, assignments and examinations.
2. MathRider (
https://mathrider.dev.java.net/)
Top of Page
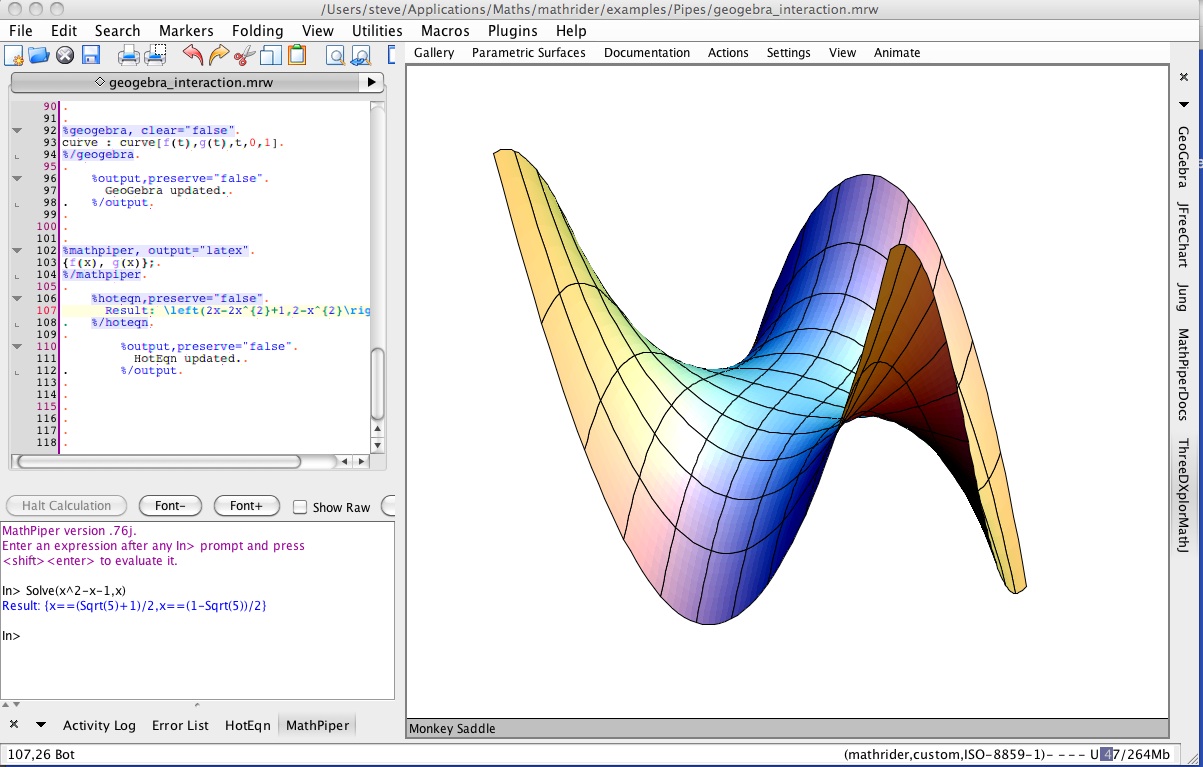
We are all familiar with the excellent GeoGebra software, which is getting better and better all the time, but what if we could add to it the useful things that it is missing? The idea of collecting together into one package a range of powerful open source software tools has been around within the Sage Project (http://www.sagemath.org) for some time. While Sage tends to be aimed at university level mathematics, the MathRider project has grown out of it, and is directly aimed at school mathematics. Freely available for Windows, OS X and Linux, this is a powerful collection of mathematical tools.
Combining GeoGebra with a growing open source computer algebra system (called MathPiper) along with a variety of other useful packages (including the quite beautiful 3D-Xplore), MathRider is an extraordinary achievement, and continues to be developed. The real challenge probably lies on getting GeoGebra to play nicely with the CAS, so that they can truly work together, and the scripting environment provided has come a long way towards achieving that harmony.
Using the scripting environment, we are able to define points A, B and C in GeoGebra, construct the dilation points that define our parametric curve and even express the functions in nice 2D display. What is missing is a true integration, in which, for example, we could move the points A, B and C in GeoGebra and have the algebraically defined curve follow this movement.
As an integrated mathematical tool, this package goes well beyond GeoGebra and is well worth taking the time to get to know. Of course, in the end, it suffers from being an amalgamation of different packages, each with their own syntax, rules, commands and purpose. Its presentation and syntax make it too difficult for most school students, at least at this stage. The free and open source offerings are always worth investigating, but for a truly integrated package which effectively offers the complete mathematical toolkit required for schools, it is hard to go past Texas Instruments' TI-Nspire.
Top of Page
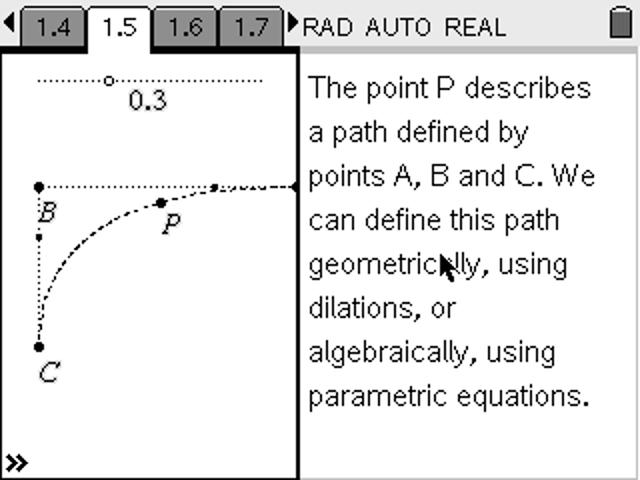
The beauty of a fully consistent interface which offers an integrated and complete mathematical toolkit is better appreciated when one has experienced the alternatives. TI-Nspire (and TI-Nspire CAS, the computer algebra system version) offer both cross-platform software as well as handheld options.
The document-based model upon which this software is based allows teachers and students to create records of their work and their mathematical thinking, step-by-step instructions, even assignments which combine text with live mathematics.
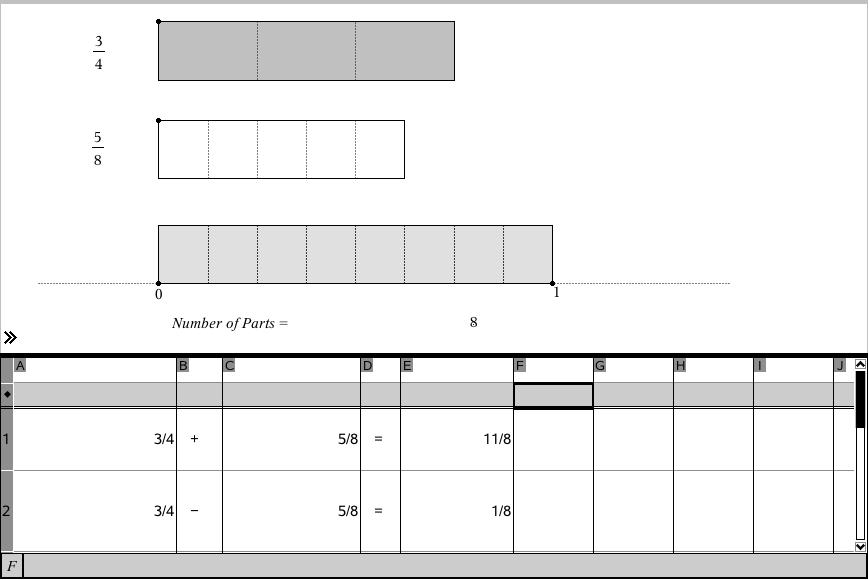
The interactivity of this tool makes it entirely appropriate for students at all levels to engage in mathematics from number, algebra geometry, statistics and more. The environments are dynamically linked, which means that student interaction in one representation is immediately reflected in other worlds.
This is a truly beautiful mathematical tool that supports not just the day-to-day classroom requirements but well beyond. With the growing range of support materials freely available online (including syllabus-linked New South Wales resources at
http://compasstech.com.au/nsw/), there is no better tool through which students may engage actively with their mathematics and it continues to get better and better.
©2009 Compass Learning Technologies ←MANSW 2009
Top of Page