©2009 Compass Learning Technologies ← NSW CAS: MANSW 2009

What might CAS mean for NSW?
Steve Arnold (steve@compasstech.com.au)

What would it mean for your students if they had access to a Computer Algebra System (CAS) for last year's Higher School Certificate Mathematics examination? What "unfair" advantage would such access offer? How much of the paper (and the course behind it) becomes trivial? These are the questions examined here.

CAS comes in both software and handheld forms. Like graph plotters and tables of values, CAS extends the mathematical toolkit available for the teaching and learning of mathematics. While a graph plotter is a representational tool (making algebraic forms visible to learners), computer algebra is manipulative, just like a normal calculator. Instead of manipulating numbers, however, CAS supports the manipulation of symbols. Most of the algebra we do in schools involves expressing algebraic forms in different (and usually equivalent) ways - simplifying, substituting, solving and, later, differentiating and integrating. So a computer algebra system is a tool that accepts symbolic (algebraic forms) and does things to transform these - simplifying, solving, expanding, factoring and more.

While scientific calculators are now largely accepted as an important part of the assumed mathematical toolkit in our state, the resistance against computer algebra systems, both here and elsewhere, remains strong. "What will be left to teach if students have access to tools that solve, factorise, differentiate, and so on?" And, more importantly, "What will be left to assess?"

It is common to hear teachers of mathematics express serious concern about student access to such tools, and the primary assumption appears to be that if students use such tools, then they will no longer need to know how to do most of the mathematics that is required of them in the secondary school and beyond. Just as scientific calculators are blamed for a decrease in numeracy skills, so CAS is predicted to lead inevitably to a loss of algebraic skill.

In this discussion, we put this assumption to the test, by examining the impact of CAS upon the Mathematics paper for the 2008 HSC. According to the concerns identified above, we might expect that such access will make most (if not all) of this paper trivial; students will need only enter the questions into the "magical" device and the answers will be delivered to them. Let us see how true this is. We will assume a student who knows how to use the CAS but does NOT know the mathematics behind these questions!
Solutions to these questions using CAS:

           

Top of Page

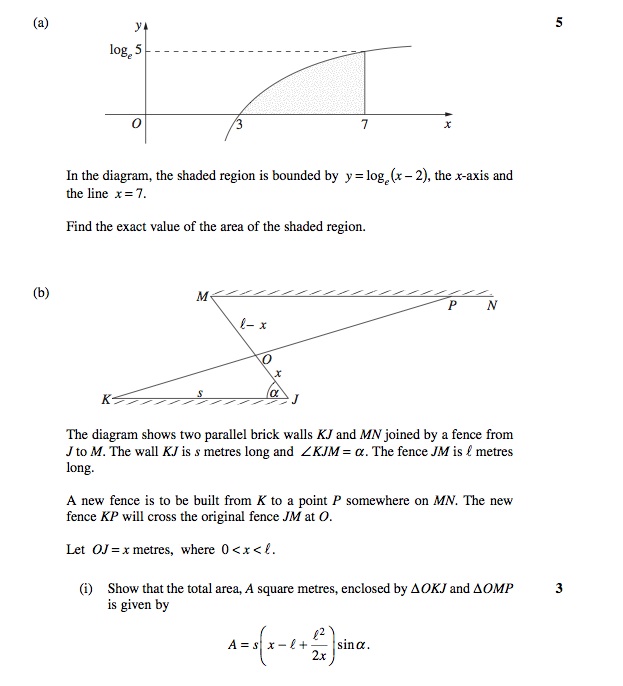
Certainly, some of these questions are made trivial - but not all! Even Question 1(a), in its demand for 3 significant figures, would see our student probably score only 1 out of 2, since the CAS will output the exact value or, if prompted for an approximate answer, will deliver several decimal places.

Question 1(c) requires the application of a fraction command to express the result in the required form, and the last question requires quite substantial interpretation of the information in the question to put it into the required form.

In other words, quite a bit of mathematical knowledge is required in addition to technical knowledge to answer these questions! And these are probably the easiest questions on the paper!

I am considering three categories in our analysis of this paper:

  1. Questions made TRIVIAL through access to CAS (requiring negligible mathematical knowledge)
  2. Questions where such access offers some real ADVANTAGE (but require mathematical knowledge as well as technical knowledge)
  3. Questions where access to CAS offers NO ADVANTAGE.

We might place questions 1(a) and 1(f) in category 2 (and award half marks for our student using CAS), and the rest in the trivial category. So our CAS-enabled student might score 10 out of 12 on question 1.


And our CAS solutions...


Top of Page

By our classifications, question 2(b) requires quite substantial mathematical expertise - there are no in-built facilities for this type of task (although they may readily be programmed - but we are assuming a blank device here). The rest of the questions would again be trivial work, and so our student again might be awarded 10 out of 12 for this question.

So far the concerns about CAS trivialising our mathematics examination seem justified, although it has always seemed to me that, if a question can be made trivial through access to technology, then that question was trivial to start with.

Top of Page

While the last two questions easily fall into the "Trivial" category, the rest were like pulling teeth - they require both a high level of technical know-how and a high level of mathematical know-how to evaluate. The in-built facilities of the device do not include even the distance formula - these need to be learned and entered correctly by the user.

Here we might concede 4 marks to be trivial; the remaining 8 marks might be considered to be advantaged by CAS, but this would be open to some debate.

We see that by this stage of the paper, the student needs to know their algebraic formulas and manipulations quite thoroughly. Where the CAS assists them is in the very mundane aspects of each task, as well as straight rote learning or manipulative skill questions.

This is the pattern that now persists throughout the remainder of the paper. Occasional questions made trivial, many questions advantaged by CAS access ONLY when combined with the required mathematical skills and knowledge, and remaining questions not affected either way.

Question 4:

Top of Page

While increasingly we are seeing computer algebra systems bundled with interactive geometry tools, such functionality is very unlikely to prove of any advantage in an examination situation. Constructions would be too time-consuming and probably too difficult for students to find any benefit in attempting them. Hence, in question 4, we might assume the first 2 marks to be non-advantaged by CAS access; the remainder of the questions are not made trivial in any sense since they must be interpreted correctly using required mathematical knowledge.

Top of Page

Similarly, there are no trivial marks in Question 5 - all require interpretation and mathematical skills and knowledge in order to arrive at the correct result. In the interests of time and space, we might move right to the last question of the paper, since it should now be relatively easy to analyse the remaining questions according to our criteria.

Traditionally, as the student progresses through the paper, the questions become increasingly heavy in interpretation - there will still be the occasional "mechanical" question (Questions 6(a) and 7(a) are "trivial") but the remaining marks are hard won, whether holding a CAS or not.

Question 10:

Top of Page

Consider the complete CAS-enabled solutions to Question 10, part (b).

Top of Page


Top of Page


Top of Page


You might observe that the CAS access for these questions would be of significant benefit to the teacher, offering worked solutions to the paper, but of little or no advantage to a student who did not know their work thoroughly.

Top of Page


And that really sums the entire exercise up, I believe.

Yes, there would be questions that we currently ask that would be made trivial if our students had access to CAS in their examinations, but these are relatively few and far between, and affect only the most mechanical parts of the course. 

In fact, by my rough calculation,
  • around 18% of this paper is unaffected by access to CAS (or graphic calculators in general)
  • approximately 36% of the paper is made trivial, and
  • some 46% is advantaged when required mathematical knowledge is present.

The greater part of the paper, with or without CAS, requires that the students' mathematical knowledge and skills are of equally high standards. Where the advantage arises is in the "mechanical" aspects of applying this knowledge and skills. The students most advantaged by CAS would be those who know their mathematics very well, but make technical errors when using their knowledge. CAS scaffolds the manipulative aspects of these tasks, allowing students to focus on interpretation and understanding of the mathematics involved, while relieving the manipulative burden.

Perhaps now we might begin to understand why, wherever CAS has been accepted into high stakes assessment, as well as consistently in the results of research, access to CAS is NOT found to be associated with a diminishing of algebraic skill. Instead, it is found that students need a higher level of understanding and ability to apply their knowledge and skills in a CAS-enabled environment than in a technology-neutral situation. Monkeys cannot be trained to use CAS.

What is achieved in a CAS-enabled curriculum is a much greater and effective focus on the higher mathematical skills of interpretation and understanding away from a focus upon pure manipulative facility, WITHOUT loss of algebraic skill - and surely that is a good thing if we are setting our students up for effective use of mathematics in life and career?

           

©2009 Compass Learning Technologies ←MANSW 2009

Top of Page