Intro
Assessment
Email
Send to Web
QR Code
Send to Cloud

Back to Top

Steve Arnold, 2018, Created with GeoGebra

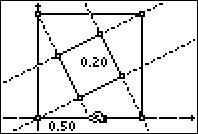
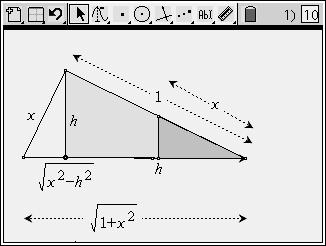
This problem may also be modelled using CabriJr on the TI-83/84 series calculator. Click on the graphic below to download the file and try it yourself!

Try having students work in pairs: one generating data points using the CabriJr model and the partner entering these into lists to plot and then to help build their algebraic model!

Just wait until you try this with TI-nspire CAS!

And you really should have a look at GXWeb and Geometry Expressions.

Back to Top

This dynamic figure was created using the latest version of the free GXWeb from Saltire Software, as shown below.

Back to Top

Solve this problem using GXWeb.

See a complete solution to this problem.

Back to Top

©2019 Compass Learning Technologies ← Live Mathematics on the Web ← GeoGebra Showcase ← The Case of the Diminishing Square