icon means there is a Things to do investigation at the
end of the section.
This, the first, looks at the Fibonacci numbers and why they appear in various "family trees" and patterns of spirals of leaves and seeds.
The second page then examines why the golden section is used by nature in some detail, including animations of growing plants.
The
icon means there is a Things to do investigation at the
end of the section.
|
The original problem that Fibonacci investigated (in the year 1202) was about how fast rabbits could breed in ideal circumstances.
Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was...
How many pairs will there be in one year?
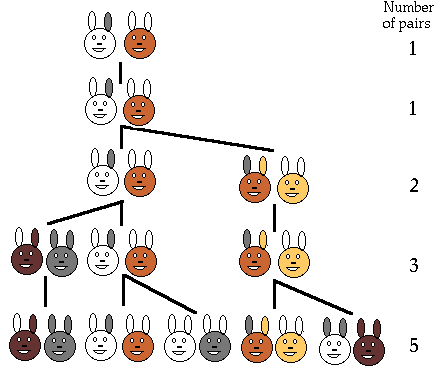
The number of
pairs of rabbits in the field at the start of each month is 1, 1, 2, 3, 5, 8,
13, 21, 34, ...
Can you see how the series is formed and how it continues? If not, look at the answer!
The first 300 Fibonacci numbers are here and some questions for you to answer.
Now can you see why this is the answer to our Rabbits problem? If not,
here's
why.
Another view of the Rabbit's Family Tree:
|
It seems to imply that brother and sisters mate, which, genetically, leads to
problems. We can get round this by saying that the female of each pair mates
with any male and produces another pair.
Another problem which again is not
true to life, is that each birth is of exactly two rabbits, one male and one
female.
He changes months into years and rabbits into bulls (male) and cows (females)
in problem 175 in his book 536 puzzles and Curious Problems (1967,
Souvenir press): 
If a cow produces its first she-calf at age two years and after that produces another single she-calf every year, how many she-calves are there after 12 years, assuming none die?This is a better simplification of the problem and quite realistic now.
But Fibonacci does what mathematicians often do at first, simplify the
problem and see what happens - and the series bearing his name does have
lots of other interesting and practical applications as we see later.
So let's look at another real-life situation that is exactly modelled by
Fibonacci's series - honeybees.
Amusements
in Mathematics, Dover Press, 1958, 250 pages. 536
Puzzles and Curious Problems is now out of print, but you may be able to
pick up a second hand version by clicking on this link. It is another collection
like Amusements in Mathematics (above) but containing different puzzles
arranged in sections: Arithmetical and Algebraic puzzles, Geometrical puzzles,
Combinatorial and Topological puzzles, Game puzzles, Domino puzzles, match
puzzles and "unclassified" puzzles. Full solutions and index. A real treasure.
The
Canterbury Puzzles, Dover 2002, 256 pages. More puzzles (not in the previous
books) the first section with some characters from Chaucer's Canterbury
Tales and other sections on the Monks of Riddlewell, the squire's Christmas
party, the Professors puzzles and so on and all with full solutions of course!
There are over 30,000 species of bees and in most of them the bees live
solitary lives. The one most of us know best is the honeybee and it, unusually,
lives in a colony called a hive and they have an unusual Family Tree. In fact,
there are many unusual features of honeybees and in this section we will show
how the Fibonacci numbers count a honeybee's ancestors (in this section a "bee"
will mean a "honeybee").
First, some unusual facts about honeybees such as:
not all of them have two parents!
In a colony of honeybees
there is one special female called the queen. There are
many worker bees who are female too but unlike the queen bee, they
produce no eggs. There are some drone bees who are male and do no
work.
Males are produced by the queen's unfertilized eggs, so male bees only
have a mother but no father! All the females are produced
when the queen has mated with a male and so have two parents. Females usually
end up as worker bees but some are fed with a special substance called royal
jelly which makes them grow into queens ready to go off to start a new
colony when the bees form a swarm and leave their home (a hive) in
search of a place to build a new nest.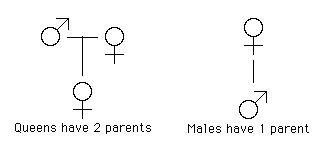
So female bees have 2 parents, a male and a female whereas male bees have just one parent, a female.
Here we follow the convention of Family Trees that parents
appear above their children, so the latest generations are at the bottom and
the higher up we go, the older people are. Such trees show all the
ancestors (predecessors, forebears, antecedents) of the person at the
bottom of the diagram. We would get quite a different tree if we listed all the
descendants (progeny, offspring) of a person as we did in the rabbit
problem, where we showed all the descendants of the original pair.
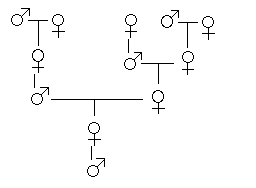Let's look at the family tree of a male drone bee.
Again we see the Fibonacci
numbers :
great- great,great gt,gt,gt
grand- grand- grand grand
Number of parents: parents: parents: parents: parents:
of a MALE bee: 1 2 3 5 8
of a FEMALE bee: 2 3 5 8 13
The Fibonacci Sequence as it appears in Nature by S.L.Basin in
Fibonacci Quarterly, vol 1 (1963), pages 53 - 57.
|
Things to do
Make a diagram of Family Tree Names so that "Me" is at the bottom and "Mum"
and "Dad" are above you. Mark in "brother", "sister", "uncle", "nephew" and as
many other names of (kinds of) relatives that you know. It doesn't matter if
you have no brothers or sisters or nephews as the diagram is meant to show the
relationships and their names.
[If you have a friend who speaks a foreign
language, ask them what words they use for these relationships.]
The Family Tree of humans involves a different sequence to the Fibonacci Numbers. What is this sequence called?
Looking at
your answers to the previous question, your friend Dee Duckshun says to you:
|
If we take the ratio of two successive numbers in Fibonacci's series, (1, 1,
2, 3, 5, 8, 13, ..) and we divide each by the number before it, we will find the
following series of numbers:
It is easier to see what is happening if we plot the ratios on a graph:
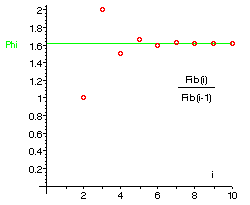
The ratio seems to be settling down to a particular value, which we call the golden ratio or the golden number. It has a value of approximately 1·618034 , although we shall find an even more accurate value on a later page [this link opens a new window] .
Things to do
|
. The
closely related value which we write as phi with a small "p" is just the
decimal part of Phi, namely 0·618034.
We can make another picture showing the Fibonacci numbers
1,1,2,3,5,8,13,21,.. if we start with two small squares of size 1 next to each
other. On top of both of these draw a square of size 2 (=1+1).
We can now draw a new square - touching both a unit square and the latest
square of side 2 - so having sides 3 units long; and then another touching both
the 2-square and the 3-square (which has sides of 5 units). We can continue
adding squares around the picture, each new square having a side which is as
long as the sum of the latest two square's sides. This set of rectangles
whose sides are two successive Fibonacci numbers in length and which are
composed of squares with sides which are Fibonacci numbers, we will call the
Fibonacci Rectangles. 
Here is a spiral drawn in the squares, a quarter of a circle in each
square. The spiral is not a true mathematical spiral (since it is made up
of fragments which are parts of circles and does not go on getting smaller and
smaller) but it is a good approximation to a kind of spiral that does appear
often in nature. Such spirals are seen in the shape of shells of snails and sea
shells and, as we see later, in the arrangment of seeds on flowering plants too.
The spiral-in-the-squares makes a line from the centre of the spiral increase by
a factor of the golden number in each square. So points on the spiral are 1.618
times as far from the centre after a quarter-turn. In a whole turn the points on
a radius out from the center are 1.6184 = 6.854 times further out
than when the curve last crossed the same radial line.
| Here is a cross-section of a Nautilus sea shell. It shows the spiral curve of the shell and the internal chambers that the animal using it adds on as it grows. The chambers provide boyancy in the water. Click on the picture to enlarge it in a new window. Draw a line from the center out in any direction and find two places where the shell crosses it so that the shell spiral has gone round just once between them. The outer crossing point will be 1.618 times as far from the centre showing that the shell has grown by a factor of the golden ratio in one turn. |  Nautilus Buy This Art Print At AllPosters.com |
 Sliced Nautilus Shell Buy This Art Print At AllPosters.com |
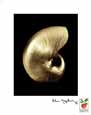 Nautilus Shell Buy This Art Print At AllPosters.com |
 Nautilus Buy This Art Print At AllPosters.com |
The curve of this shell is called Equiangular
or Logarithmic spirals
and are common in nature, though the 'growth factor' may not always be the
golden ratio.
Reference
A Dover reprint of a classic 1914 book.
|
|
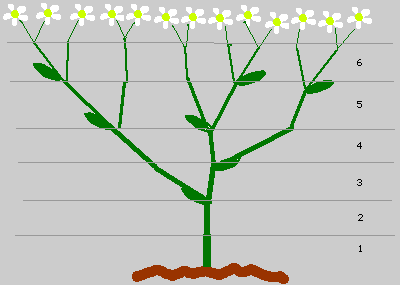
One plant in particular shows the Fibonacci numbers in the number of "growing points" that it has. Suppose that when a plant puts out a new shoot, that shoot has to grow two months before it is strong enough to support branching. If it branches every month after that at the growing point, we get the picture shown here.
A plant that grows very much like this is the "sneezewort": Achillea ptarmica.
|
On many plants, the number of petals is a Fibonacci number:
buttercups
have 5 petals; lilies and iris have 3 petals; some delphiniums have 8; corn
marigolds have 13 petals; some asters have 21 whereas daisies can be found with
34, 55 or even 89 petals.
The links here are to various flower and plant
catalogues:
 Fuchsia |
 Pinks |
 Lily |
 Daisies available as a poster at AllPosters.com |
Here is a passion flower (passiflora incarnata) from the back and front:
|
 |
| Back view: the 3 sepals that protected the bud are outermost, then 5 outer green petals followed by an inner layer of 5 more paler green petals |
Front view: the two sets of 5 green petals are outermost, with an array of purple-and-white stamens (how many?); in the centre are 5 greenish stamens (T-shaped) and uppermost in the centre are 3 deep brown carpels and style branches) |
|
This poppy seed head has 13 ridges on top. 
Fibonacci numbers can also be seen in the arrangement of seeds on flower heads. The picture here is Tim Stone's beautiful photograph of a Coneflower, used here by kind permission of Tim. The part of the flower in the picture is about 2 cm across. It is a member of the daisy family with the scientific name Echinacea purpura and native to the Illinois prairie where he lives.
You can have a look at some more of Tim's wonderful photographs on the web. 
You can see that the orange "petals" seem to form spirals curving both to the left and to the right. At the edge of the picture, if you count those spiralling to the right as you go outwards, there are 55 spirals. A little further towards the centre and you can count 34 spirals. How many spirals go the other way at these places? You will see that the pair of numbers (counting spirals in curing left and curving right) are neighbours in the Fibonacci series. Click on the picture on the right to see it in more detail in a separate window.
On the left is a real sunflower with 89 and 55 spirals at the edge.
 Sunflower Buy This Art Print At AllPosters.com |
Here are some more wonderful pictures from All Posters (which you can buy for your classroom or wall at home). Click on each to enlarge it in a new window. |  SunflowerBuy This Poster At AllPosters.com |
The same happens in many seed and flower heads in nature. The reason seems to be that this arrangement forms an optimal packing of the seeds so that, no matter how large the seed head, they are uniformly packed at any stage, all the seeds being the same size, no crowding in the centre and not too sparse at the edges.
The spirals are patterns that the eye sees, "curvier" spirals appearing near the centre, flatter spirals (and more of them) appearing the farther out we go.So the number of spirals we see, in either direction, is different for
larger flower heads than for small. On a large flower head, we see more spirals
further out than we do near the centre. The numbers of spirals in each direction
are (almost always) neighbouring Fibonacci numbers! Click on these links
for some more diagrams of 500, 1000 and 5000 seeds.
Click on the image on the right for a Quicktime animation of 120
seeds appearing from a single central growing point. Each new seed is just phi
(0·618) of a turn from the last one (or, equivalently, there are Phi (1·618)
seeds per turn). The animation shows that, no matter how big the seed head gets,
the seeds are always equally spaced. At all stages the Fibonacci Spirals can be
seen.
The same pattern shown by these dots (seeds) is followed if the dots then develop into leaves or branches or petals. Each dot only moves out directly from the central stem in a straight line.
This process models what happens in nature when the "growing tip" produces seeds in a spiral fashion. The only active area is the growing tip - the seeds only get bigger once they have appeared.
[This animation was produced by Maple. If there are N seeds in one frame, then the newest seed appears nearest the central dot, at 0·618 of a turn from the angle at which the last appeared. A seed which is i frames "old" still keeps its original angle from the exact centre but will have moved out to a distance which is the square-root of i.]
Note that you will not always find the Fibonacci numbers in the number of petals or spirals on seed heads etc., although they often come close to the Fibonacci numbers.
Things to do
Nicky's Seeds who supplies
the whole range of flower and vegetable seed including sunflower seed in the
UK.
|
Things to do
Ohio State
University Professor Susan
Goldstine
Fibonacci Statistics in Conifers A Brousseau , The Fibonacci
Quarterly vol 7 (1969) pages 525 - 532
Pineapples and Fibonacci Numbers P B Onderdonk The Fibonacci
Quarterly vol 8 (1970), pages 507, 508.
|
Also, many plants show the Fibonacci numbers in the arrangements of
the leaves around their stems. If we look down on a plant, the leaves are often
arranged so that leaves above do not hide leaves below. This means that each
gets a good share of the sunlight and catches the most rain to channel down to
the roots as it runs down the leaf to the stem.
Here's a
computer-generated image, based on an African violet type of plant, whereas
this
has lots of leaves.
The Fibonacci numbers occur when counting both the number of times we go around the stem, going from leaf to leaf, as well as counting the leaves we meet until we encounter a leaf directly above the starting one.
If we count in the other direction, we get a different number of turns for the same number of leaves.
The number of turns in each direction and the number of leaves met are three consecutive Fibonacci numbers!
For example, in the top plant in the picture above, we have 3
clockwise rotations before we meet a leaf directly above the first, passing
5 leaves on the way. If we go anti-clockwise, we need only 2
turns. Notice that 2, 3 and 5 are consecutive Fibonacci numbers.
For the
lower plant in the picture, we have 5 clockwise rotations passing
8 leaves, or just 3 rotations in the anti-clockwise direction.
This time 3, 5 and 8 are consecutive numbers in the Fibonacci sequence.
We
can write this as, for the top plant, 3/5 clockwise rotations per leaf (
or 2/5 for the anticlockwise direction). For the second plant it is 5/8 of a
turn per leaf (or 3/8).
| Leaf number |
turns clockwise |
| 3 | 1 |
| 5 | 2 |
| 8 | 3 |
One estimate is that 90 percent of all plants exhibit this pattern of leaves involving the Fibonacci numbers.
Some common trees with their Fibonacci leaf arrangement numbers are:
1/2 elm, linden, lime, grasses
1/3 beech, hazel, grasses, blackberry
2/5 oak, cherry, apple, holly, plum, common groundsel
3/8 poplar, rose, pear, willow
5/13 pussy willow, almond
where t/n means each leaf is t/n of a turn after the last leaf or that there is there are t turns for n leaves.
Cactus's spines often show the same spirals as we have already seen on pine cones, petals and leaf arrangements, but they are much more clearly visible. Charles Dills has noted that the Fibonacci numbers occur in Bromeliads and his Home page has links to lots of pictures.
|
Here is a picture of an ordinary cauliflower. Note how it is almost a pentagon in outline. Looking carefully, you can see a centre point, where the florets are smallest. Look again, and you will see the florets are organized in spirals around this centre in both directions.
How many spirals are there in each direction?
These buttons will show the spirals more clearly for you to count (lines are
drawn between the florets):
Romanesque Brocolli/Cauliflower (or Romanesco) looks and tastes like a cross between brocolli and cauliflower. Each floret is peaked and is am identical but smaller version of the whole thing and this makes the spirals easy to see.
How many spirals are there in each direction?
These buttons will show the spirals more clearly for you to count (lines are
drawn between the florets):
Things to do
Chinese leaves and lettuce are similar but there is
no proper stem for the leaves. Instead, carefully take off the leaves, from
the outermost first, noticing that they overlap and there is usually only one
that is the outermost each time. You should be able to find some Fibonacci
number connections.
|
Look at your own hand:
You have ...
Is this just a coincidence or not?????
However, if you measure the lengths of the bones in your finger (best seen by slightly bending the finger) does it look as if the ratio of the longest bone in a finger to the middle bone is Phi?Why not measure your friends' hands and gather some statistics?
|
Finally, note that, although the Fibonacci numbers and golden section seem to appear in many situations in nature, they are not the only such numbers. H S M Coxeter, in his Introduction to Geometry (1961, Wiley, page 172) - see the references at the foot of this page - has the following important quote:
He cites A H Church's The relation of phyllotaxis to mechanical laws, Williams and Norgate, London, 1904, plates XXV and IX as examples of the Lucas and the latter two sequences and plates V, VII, XIII and VI as examples of the Fibonacci numbers on sunflowers.it should be frankly admitted that in some plants the numbers do not belong to the sequence of f's [Fibonacci numbers] but to the sequence of g's [Lucas numbers] or even to the still more anomalous sequences
3,1,4,5,9,... or 5,2,7,9,16,...Thus we must face the fact that phyllotaxis is really not a universal law but only a fascinatingly prevalent tendency.
The Lucas numbers are formed in the same way as the Fibonacci numbers - by adding the latest two to get the next, but instead of starting at 0 and 1 [Fibonacci numbers] the Lucas number series starts with 2 and 1. The other two sequences Coxeter mentions above have other pairs of starting values but then proceed with the exactly the same rule as the Fibonacci numbers. These series are the General Fibonacci series.
An interesting fact is that for all series that are formed from adding the latest two numbers to get the next starting from any two values (bigger than zero), the ratio of successive terms will always tend to Phi!
So Phi (1.618...) and her sister phi (0.618...) are constants common to all varieties of Fibonacci series and they have lots of interesting properties of their own too. The links above will take you to further pages on this site for you to explore. You can also just follow the links below in the Where To next? section at the bottom on each page and this will go through the pages in order. Or you can browse through the pages that take your interest from the complete collection and brief descriptions on the home page. There are pages on Who was Fibonacci?, the golden section (phi) in the arts: architecture, music, pictures etc as well as two pages of puzzles.
|
Excellent books which cover similar material to that which you have found on this page are produced by Trudi Garland and Mark Wahl:Key
Mathematical
Mystery Tour by Mark Wahl, 1989, is full of many mathematical
investigations, illustrations, diagrams, tricks, facts, notes as well as guides
for teachers using the material. It is a great resource for your own
investigations.
Books by Trudi Garland: Fascinating
Fibonaccis by Trudi Hammel Garland.
This is a really excellent book -
suitable for all, and especially good for teachers seeking more material to use
in class.
Trudy is a teacher in California and has some more information on her
book. (You can even Buy it
online now!)
She also has published several posters, including one on the golden
section suitable for a classroom or your study room wall.
You should
also look at her other Fibonacci book too: Fibonacci
Fun: Fascinating Activities with Intriguing Numbers Trudi Hammel Garland - a
book for teachers.
Sex
ratio and sex allocation in sweat bees (Hymenoptera: Halictidae) D Yanega,
in Journal of Kansas Entomology Society, volume 69 Supplement, 1966,
pages 98-115.
Because of the imbalance in the family tree of honeybees, the
ratio of male honeybees to females is not 1-to-1. This was noticed by Doug
Yanega of the Entomology Research Museum at the University of California. In the
article above, he correctly deduced that the number of females to males in the
honeybee community will be around the golden-ratio Phi = 1.618033.. . On the Trail
of the California Pine, Brother Alfred Brousseau, Fibonacci
Quarterly, vol 6, 1968, pages 69 - 76;
on the authors summer expedition
to collect examples of all the pines in California and count the number of
spirals in both directions, all of which were neighbouring Fibonacci numbers.
Why
Fibonacci Sequence for Palm Leaf Spirals? in The Fibonacci Quarterly
vol 9 (1971), pages 227 - 244. Fibonacci System in Aroids in
The Fibonacci Quarterly vol 9 (1971), pages 253 - 263. The Aroids are a
family of plants that include the Dieffenbachias, Monsteras and Philodendrons.
Phyllotaxis - An interactive site
for the mathematical study of plant pattern formation by Pau Atela or
Chris Golé of the Mathematics Dept at Smith College, Massachusetts.
Alan
Turing
The book Alan
Turing: The Enigma by Andrew Hodges is an enjoyable and readable account
of his life and work on computing as well as his contributions to solving the
German war-time code which used a machine called "Enigma". The most
irrational number
Phyllotaxis
| There are no earlier topics - this is the first. |  the
Fibonacci Home Page
This is the first page on this Topic.
Where to now? The next page on this topic is ... | The next Topic is... The
Puzzling World of Fibonacci Numbers |
©
1996-2003 Dr Ron
Knott 
updated 16 October 2004 
