Making Algebra Meaningful With Technology

Stephen ARNOLD
Home →Making Algebra Meaningful with Technology

Making Algebra Meaningful With Technology

Stephen Arnold

Download in PDF format

Download Meaningful Algebra Collection (zipped, ~350 KB)

Introduction

1. Begin with number

2. Introduce graphs carefully

3. Build firm concrete foundations

4. Build Algebraic Meaning using Real Language

5. Use Appropriate Tools and Representations

6. Bring it all together with modelling

Conclusion

Introduction
Top of Page

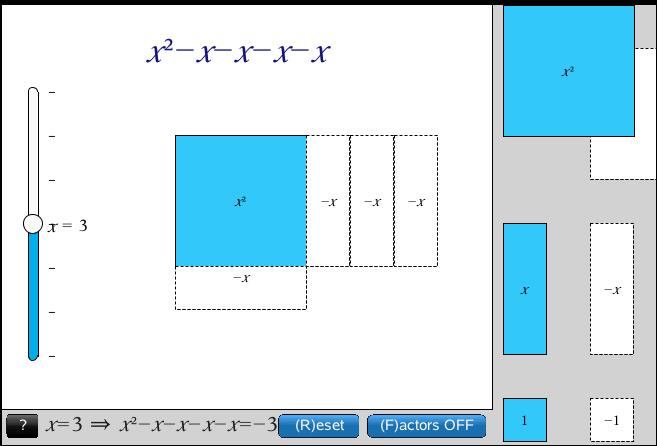
What does 2x + 1 mean to you?

What dominant image springs to mind?

Do you see an object or a process?

Do you think of a graph? A table of values?

Students who are successful in algebra have a rich repertoire of images compared to those who do not. As teachers, we need to build these images deliberately and with care.


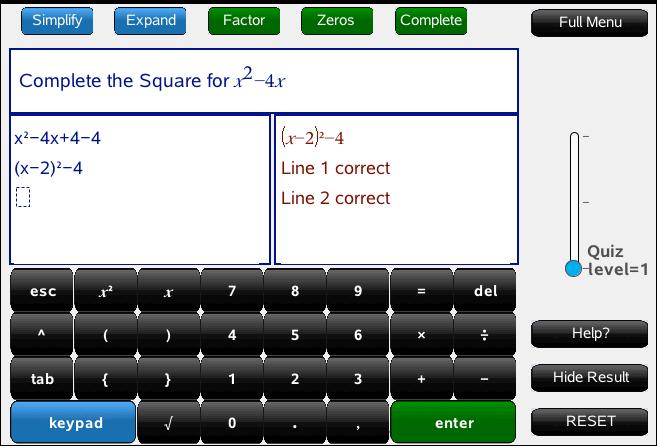
1. Begin with Number
Top of Page

School algebra is, by its nature, firmly grounded in number. It is a generalization of the rules which we apply when working with numbers. Beginning with patterns firmly associates an active "process" image with algebraic forms rather than the static "object" way of thinking. 2x + 1 is a series of instructions rather than a "blob".

In this simple activity, the teacher may enter a function on the following graph page, unseen by the students. Returning to the spreadsheet, they try to work out the rule for the pattern they see. The teacher may prompt them - the pattern is of the form "a*x + b", for example. They quickly begin to notice that the y-values increase by the same amount each time, and the y-value when x = 0 is significant.

The game becomes more interesting when, instead of entering the simplest form (such as "2x+1") the teacher enters some variation - "x + 1 + x". Then as students guess the correct rule (2x+1) the teacher can say, "Yes, that rule does work. But it is not what I have!" This is a great motivator - after a few turns with the class, students may even challenge each other in pairs!



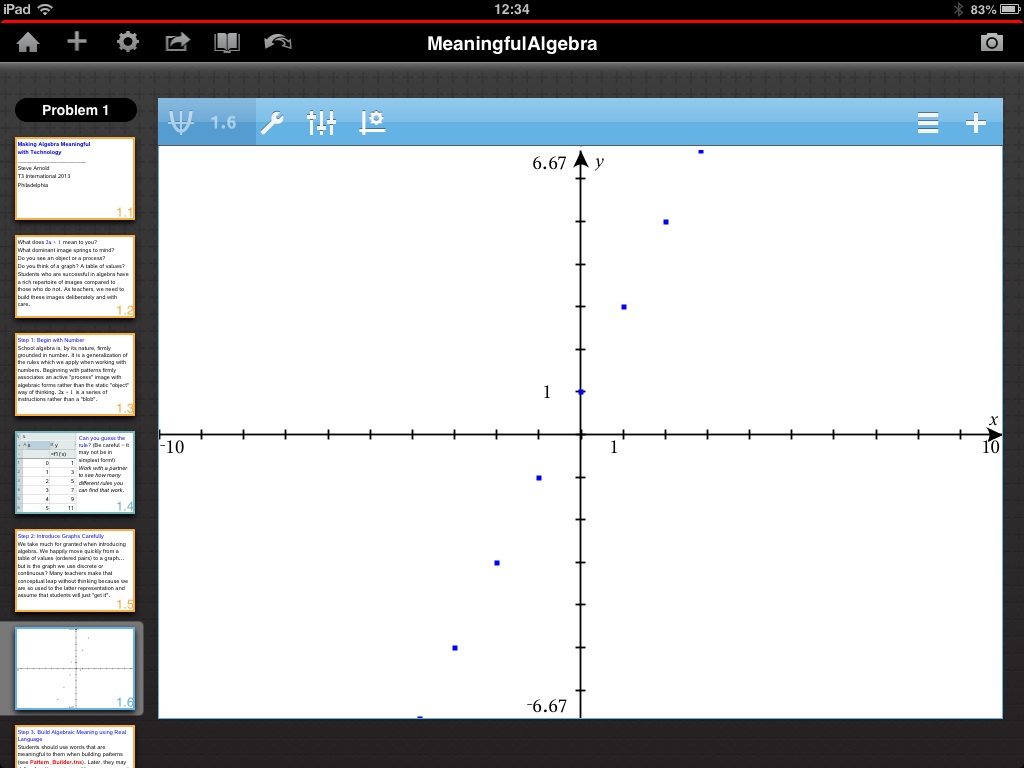
2. Introduce Graphs Carefully
Top of Page

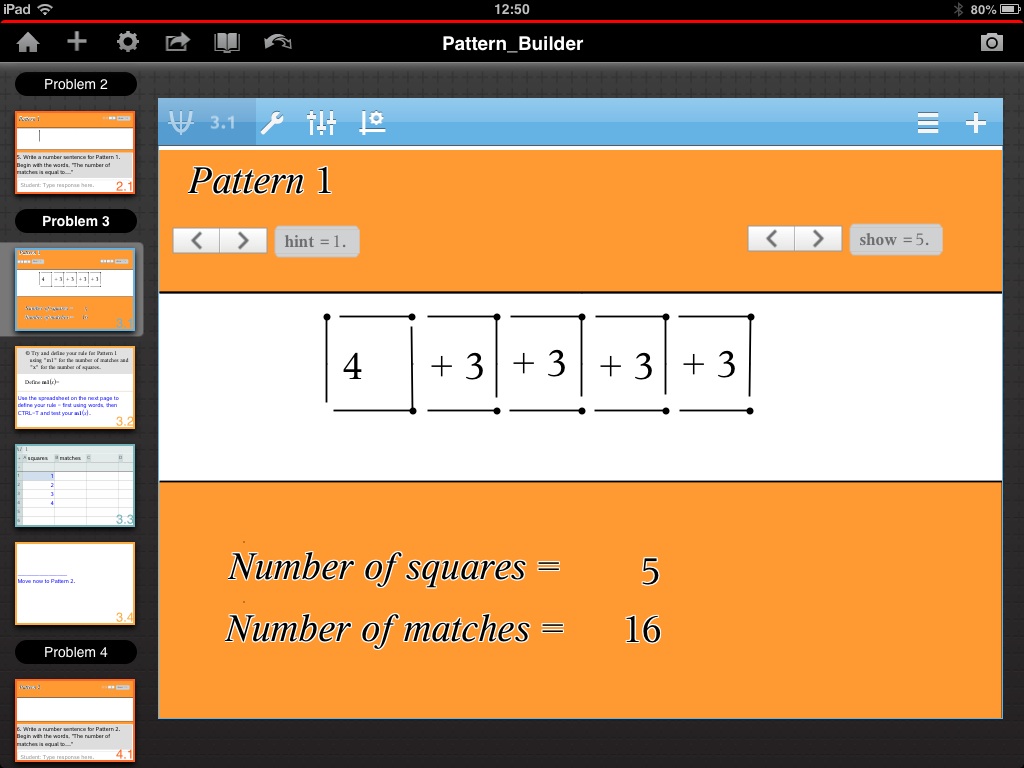
We take much for granted when introducing algebra. We happily move quickly from a table of values (ordered pairs) to a graph... but is the graph we use discrete or continuous? Many teachers make that conceptual leap without thinking because we are so used to the latter representation and assume that students will just "get it".



3. Build Algebraic Meaning using Real Language
Top of Page

Students should use words that are meaningful to them when building patterns (see Pattern_Builder.tns). Later, they may define functions using real language, even at higher levels. "Perfect problems" such as the paper fold, and the falling ladder illustrate this powerful approach well. These are explored further under modelling.



4. Build Firm Concrete Foundations
Top of Page

Concrete manipulatives ("algebra tiles") can be a powerful tool for building deep understanding, and the virtual variety are actually a major improvement: they explicitly link the shapes to the symbolic form, and they establish that variables are dynamic rather than static things. Take time to explore Visual_Algebra.tns.


5. Use Appropriate Tools and Representations
Top of Page

The Visual Algebra suite illustrates how, having established meaning behind algebraic objects, students may learn to act upon these in powerful ways. Suitable scaffolding and direction builds both conceptual understanding and manipulative skill.

The model here seeks to address some of the key issues encountered with common tools for doing and learning mathematics using technology (especially CAS, initially designed for mathematicians and engineers, not for students!).

First, students need to recognize a "mathematical object" (equation, expression, graph...) from a given problem situation (this could be a real world context or as simple as a textbook question). Once an object has been identified, it must be correctly entered into the tool. An approach taken here is to use algebra tiles as the medium for entry of algebraic forms. They serve well for linear and quadratic functions - and these are exactly the functions that are critical in the first years of algebra study. In this implementation, immediate feedback is also provided as the expression is entered. So why not use this visual and tactile approach as an input method for our CAS? Of course, you can still enter expressions and equations in the usual way, directly into the CAS page provided, but this approach seems to offer substantial promise for students to build their algebraic objects - and then to be able to act meaningfully upon them.

Once the mathematical object has been entered and verified as correct, the next student stumbling block occurs - what to do with this object? This is no small problem. Modern CAS offer a bewildering array of commands (and always have, actually). Menu after menu offer multiple options which prove confusing for many students. In the prototype shown, as the object is entered, the range of available actions (limited here considerably) is further reduced to those appropriate for that particular object. The full range of actions can be accessed at any time, but this reduction of complexity is an important attribute of this model.

On selecting an action, the "plain english" form is displayed - in the example shown, "Complete the Square" is displayed so that students may readily relate the object and the action. As soon as an algebraic form is entered, the graphical and tabular forms are also available on the next page. The linking of representations for early learners remains critically important, but it also must be managed carefully by the teacher. Making such forms available on the next page offers such control.

Additionally, an experimental "motion explorer" is offered, linking the current function or equation to the movement of runners in a "race". Direct control over the motion is offered through grabbing and dragging the graph - changing y-intercept and gradient in particular. This adds another powerful and perhaps unexpected dimension to the students' thinking about that algebraic object.



6. Bring it all together with Modelling
Top of Page

Once we have built firm numerical foundations for symbol and graph, our students are ready to begin to use algebra – perhaps a novel idea in current classrooms! The real power of algebra lies in its use as a tool for modeling the real world (and, in fact, all possible worlds!) research is clear that students in the middle years of schooling (which is when we introduce algebra) most strongly need their mathematics to be relevant and significant to their lives. Teaching algebra from a modeling perspective most clearly exemplifies that approach, and serves to bring together the symbols, numbers and graphs that they have begun to use.

As mentioned above, a few "perfect problems" might be an ideal place to start!



7. Conclusion
Top of Page

Why do I like to use technology in my Mathematics teaching?

It helps my students to be better learners:

o     It scaffolds their learning, allowing them to see more and to reach further than would be possible unassisted

o     Good technology extends and enhances their mathematical abilities, potentially offering a more level playing field for all

o     It is inherently motivating, giving them more control over both their mathematics and the ways that they may learn it

o     Good technology encourages them to ask more questions about their mathematics, and offers insight into the true nature and potential of mathematical thinking and knowledge

Good technology also helps me to be a better teacher:

o     It offers better ways of teaching, new roads to greater understanding than was previously possible

o     It encourages me to talk less and to listen more: Students and teacher tend to become co-learners

o     It makes my students’ thinking public, helping me to better understand their strengths and weaknesses, and to better evaluate the quality of my own teaching and of their learning

o     It frequently renews my own wonder of Mathematics, helping me to think less like a mathematics teacher and more like a mathematician

Why do I love using technology in my mathematics classroom?

Because, like life, mathematics was never meant to be a spectator sport.

Top of Page

For comments & suggestions, please e-mail Steve Arnold.

Back to My Home Page

1. Begin with Number Top of Page School algebra is, by its nature, firmly grounded in number. It is a generalization of the rules which we apply when working with numbers. Beginning with patterns firmly associates an active "process" image with algebraic forms rather than the static "object" way of thinking. 2x + 1 is a series of instructions rather than a "blob". In this simple activity, the teacher may enter a function on the following graph page, unseen by the students. Returning to the spreadsheet, they try to work out the rule for the pattern they see. The teacher may prompt them - the pattern is of the form "a*x + b", for example. They quickly begin to notice that the y-values increase by the same amount each time, and the y-value when x = 0 is significant. The game becomes more interesting when, instead of entering the simplest form (such as "2x+1") the teacher enters some variation - "x + 1 + x". Then as students guess the correct rule (2x+1) the teacher can say, "Yes, that rule does work. But it is not what I have!" This is a great motivator - after a few turns with the class, students may even challenge each other in pairs!
2. Introduce Graphs Carefully Top of Page We take much for granted when introducing algebra. We happily move quickly from a table of values (ordered pairs) to a graph... but is the graph we use discrete or continuous? Many teachers make that conceptual leap without thinking because we are so used to the latter representation and assume that students will just "get it".
3. Build Algebraic Meaning using Real Language Top of Page Students should use words that are meaningful to them when building patterns (see Pattern_Builder.tns). Later, they may define functions using real language, even at higher levels. "Perfect problems" such as the paper fold, and the falling ladder illustrate this powerful approach well. These are explored further under modelling.
4. Build Firm Concrete Foundations Top of Page Concrete manipulatives ("algebra tiles") can be a powerful tool for building deep understanding, and the virtual variety are actually a major improvement: they explicitly link the shapes to the symbolic form, and they establish that variables are dynamic rather than static things. Take time to explore Visual_Algebra.tns. 5. Use Appropriate Tools and Representations Top of Page The Visual Algebra suite illustrates how, having established meaning behind algebraic objects, students may learn to act upon these in powerful ways. Suitable scaffolding and direction builds both conceptual understanding and manipulative skill. The model here seeks to address some of the key issues encountered with common tools for doing and learning mathematics using technology (especially CAS, initially designed for mathematicians and engineers, not for students!). First, students need to recognize a "mathematical object" (equation, expression, graph...) from a given problem situation (this could be a real world context or as simple as a textbook question). Once an object has been identified, it must be correctly entered into the tool. An approach taken here is to use algebra tiles as the medium for entry of algebraic forms. They serve well for linear and quadratic functions - and these are exactly the functions that are critical in the first years of algebra study. In this implementation, immediate feedback is also provided as the expression is entered. So why not use this visual and tactile approach as an input method for our CAS? Of course, you can still enter expressions and equations in the usual way, directly into the CAS page provided, but this approach seems to offer substantial promise for students to build their algebraic objects - and then to be able to act meaningfully upon them. Once the mathematical object has been entered and verified as correct, the next student stumbling block occurs - what to do with this object? This is no small problem. Modern CAS offer a bewildering array of commands (and always have, actually). Menu after menu offer multiple options which prove confusing for many students. In the prototype shown, as the object is entered, the range of available actions (limited here considerably) is further reduced to those appropriate for that particular object. The full range of actions can be accessed at any time, but this reduction of complexity is an important attribute of this model. On selecting an action, the "plain english" form is displayed - in the example shown, "Complete the Square" is displayed so that students may readily relate the object and the action. As soon as an algebraic form is entered, the graphical and tabular forms are also available on the next page. The linking of representations for early learners remains critically important, but it also must be managed carefully by the teacher. Making such forms available on the next page offers such control. Additionally, an experimental "motion explorer" is offered, linking the current function or equation to the movement of runners in a "race". Direct control over the motion is offered through grabbing and dragging the graph - changing y-intercept and gradient in particular. This adds another powerful and perhaps unexpected dimension to the students' thinking about that algebraic object.
6. Bring it all together with Modelling Top of Page Once we have built firm numerical foundations for symbol and graph, our students are ready to begin to use algebra – perhaps a novel idea in current classrooms! The real power of algebra lies in its use as a tool for modeling the real world (and, in fact, all possible worlds!) research is clear that students in the middle years of schooling (which is when we introduce algebra) most strongly need their mathematics to be relevant and significant to their lives. Teaching algebra from a modeling perspective most clearly exemplifies that approach, and serves to bring together the symbols, numbers and graphs that they have begun to use. As mentioned above, a few "perfect problems" might be an ideal place to start!