Integrating Technology in the Middle School: Years 5-9

Stephen Arnold

Download in PDF format

 

In the past, graphic calculators have been sophisticated and exciting tools for higher mathematics, but few would have considered using them more than occasionally with younger students. All this has now changed with the growing range of software Apps now available for Texas Instruments TI-83 Plus calculators. These Apps are more like computer software than calculator programs and, in many ways, make the device more like a laptop than a calculator, especially when combined with the new keyboard, which supports the free MS-Word-compatible word processor, along with the spreadsheet, dynamic geometry and much more.

 

Rather than giving a description of some of the wonderful new Apps now freely available, my plan here is to present a number of lesson outlines which I have used with upper primary through to secondary students in the past few months. Those described here explore applications to space, data and number.

 

---

• Space: Investigating Angles
• Data1: Data, data everywhere
• Data2: Data in Motion
• Number: Curious Numbers

---

 

1. SPACE: Investigating Angles

 

AIM                      Students are provided with a variety of experiences to build their confidence and understanding related to angles, both types and estimating sizes.

 

METHOD            These activities provide a range of activities which will involve students in estimating angle sizes, and in realizing the links between angles and plane shapes.

 

PROCESS

 

This lesson (or two) uses three Apps currently available which offer superb resources for space and geometry at all levels: What’s my Angle, LOGO and CabriJr™. All are free and can be put onto any TI-83 Plus calculator.

 

Introduction (10 minutes):

 

 

What’s My Angle? is a fun and well-designed way for students to build their skills in angle estimation. Beginning with acute angles, and progressing through the different angle types, students are presented with eye-catching animations for which they must guess the angles shown. If their guess is incorrect, they are then offered a multiple-choice selection from which to choose.

 

Scores are kept and different questions asked each time the App is run. It may be used at the start of each lesson for a week or longer if desired. I have used this with classes from Year 5 to Year 12, and all loved it!

 

By the end of the introduction, students should be comfortable with the differences between acute, obtuse and reflex angles, and have some skills in guessing their sizes.

 

Robot Angles (30-40 minutes)

 

We all know what a square is, don’t we?

But what if you are a robot, who only knows four commands: forward, back, left and right? What instructions would produce a square? Having one student serve as the robot and others giving the instructions proves a powerful and effective learning mechanism, which produces surprisingly robust understandings related to distances, angles, position and direction.

 

The original LOGO computer language was designed by Seymour Papert and his team at the Massachusetts Institute of Technology over thirty years ago. It was designed around the motto “No floor, no ceiling” with its implication of accessibility for all, but the potential for learning experiences appropriate for any age. It remains a powerful environment for learning mathematics, particularly concepts and skills associated with space and geometry.

 

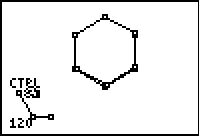
The LOGO App offers basic “turtle graphics” (the turtle is the nickname for the triangular “robot” which draws as it carries out instructions). In the case of a square, students quickly arrive at the series of commands: FD 20 (or whatever distance is appropriate), LT 90, FD 20, LT 90, FD 20, LT 90, FD 20, LT 90 (again, a right turn would have been equally correct). This may be shortened to REPEAT 4 [FD 20 LT 90].

 

This provides the starting point. Constructing a triangle always proves more difficult than expected (since the turn for an equilateral triangle is 120 degrees rather than the expected 60) but students begin to feel angles since they are physically involved in the process. This leads naturally to improved skills and concepts related to position and direction, and links directly with map reading and orienteering activities.

 

Other applications include tessellations. The pattern above was created using the command sequence: REPEAT 5 [REPEAT 3 [FD 20 LT 120] LT 60 ].

 

Every student should have the opportunity to work within the LOGO environment. In the words of its creator, it seeks to be a “mathland”, where learning the language of mathematics is as natural as learning French if you grow up in France!

What’s Your Angle? (10-20 minutes)           

 

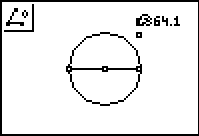
This activity introduces dynamic geometry using the new CabriJr™ App, and allows students to further explore the properties of angles.

 

Begin with a circle (F2: Circle). Press ENTER once to set the center, use the right arrow to move out and then ENTER a second time to set the radius. Use the green ALPHA key to grab the point on the circumference and resize the circle to get a feel for this dynamic geometry.

 

 

Create a symmetrical point on the opposite side of the circle, using F4: Symmetry (choose the last point, then move to the center of the circle and press ENTER). You have created a diameter.

 

Now move away from the center and create a free point (F2: Point -> Point).

 

Finally, measure the angle from one end point of the diameter, to the free point, then to the other diameter end point.

 

You may now begin to move the point around the screen, observing the way that the angle changes in relation to the position of the circle.

 

Record and discuss observations. Later, you may choose to allow students to create the triangle defined by the three points and make explicit the nature of the angle. Some students will be quite uncomfortable until this is done. Talk more about angles.

 

 

All Shapes and Sizes (20 minutes)

 

 

 

Bringing the previous activities together, this last session uses a CabriJr™ prepared file called CPOLY, in which students move a control segment, which changes the angle shown. This then changes the shape of the polygon.

 

Students are encouraged to work in pairs or small groups to investigate the relationship between the angle and the shape. They should discuss and record their observations, and then each group is to prepare a report (with diagrams) for presentation to the class.

 

 

 

2. DATA(1): Data, data Everywhere

 

AIM                      To provide students with opportunities based on their own experiences to judge the appropriate use of different types of graphs in different situations.

 

METHOD            Using data derived from their own birthdays, students create (both physically and using available technology in the form of a spreadsheet) graphs which describe this data.

 

PROCESS

 

Although graphic calculators are perhaps best known for their function graphing capabilities, in many ways it is their ability to manipulate and represent data that is far more useful and important at all levels. Students may readily enter numerical data into lists which can then be viewed using a variety of graph types, or analysed statistically with ease. Add the capabilities of a spreadsheet, and even more is possible.

 

This activity involves students with several graph types, used to represent birthday data. It is fun and motivational, since students love to be personally involved in their learning. It also engages them physically, as they begin each section by forming “people graphs”.

 

Introduction: Seasons (20 minutes)

 

Students who were born in the Spring months (September to November) are called out and  form a line. Next the summer babies (December to February) line up next to them, followed by the Autumn and Winter babies. The lines are then joined to form a circle and students sit down. They have just formed a human pie chart: each group in turn should stand and see their part in this graph, and some discussion can follow, concerning what they expected to see.

 

They may then return to their seats and create a simple spreadsheet (using the CellSheet™ App) as shown. They may use this to produce a pie chart, which can indicate both numerical values and percentage values, which can be copied into their workbooks.

 

 

 Days of the Week (20-30 minutes)

 

A small program can be used by students to calculate the day of their birth, given the date. This is always a fun activity and, again, can be used as the basis for generating data. Lining up this time as Monday, children, Tuesday children, etc, students will quickly observe that a pie chart is not really suitable for this data: too busy and confusing, too many categories.

 

Instead, line them up in parallel lines by the day of the week to form a human column graph. Once again, sit them down and have each group stand to observe the shape of the graph. Talk about the differences between these graphs and why some data is better represented by one type of graph, and other data by another graph type.

 

You may finish by having the end students of each column join hands, and talk about why a line graph is not appropriate for this type of data.

Returning to their seats, students again enter the data into the spreadsheet and view and discuss the column graph produced. Differences between a column graph and a histogram may be discussed as appropriate for the level involved.

 

It is also fun to finish with the old birthday poem (shown here using the NoteFolio App).

 

 

Finally, depending on the level of the group, it may be appropriate to extend this activity to include stem-and-leaf plots (use the day of their birth, numbers from 1 to 31, with the option to separate the boys and the girls to form a back-to-back stem-and-leaf plot); older students may even form human box-and-whisker plots, calculating their birthday as a number from 1 to 365!

 

 

3. DATA(2): Data in Motion

 

AIM                      To introduce graphs of motion and travel in an active and realistic way using a motion detector.

 

METHOD            By physically involving students in the creation of graphs, they quickly become familiar with the key ideas behind this important way of representing data.

 

PROCESS

 

The possibilities for the use of data logging in the middle school are great: there are so many ways to enhance the teaching of both mathematics and science through the use of real-world data, and one of the most immediate and yet most powerful lies in the use of the CBR™ (Calculator-Based Ranger) motion detector. This amazing device connects directly to any Texas Instruments graphic calculator and, using simple menus, presents graphs of motion created by the students.

 

 

Getting Started (10-15 minutes)

 

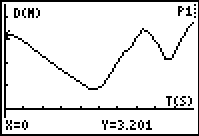
Begin with a student simply moving back and forward in a straight line in front of the CBR™, while the graph of their motion appears on the ViewScreen™ for all to see. As can be seen from the first graph, the horizontal axis displays time in seconds, the vertical axis, distance in metres (the device can also switch between Distance/Time, Velocity/Time and Acceleration/Time if desired, but it is probably sufficient to just work with Distance/Time at this point).

 

Ask a few other students to create graphs – I like to suggest that they create mountains, and then valleys, with help from their peers, who can suggest whether they begin close to the CBR™ or far away. Students quickly pick up what is happening and become confident in predicting the shapes of graphs to match a variety of motions.

 

After a couple of introductory walks, it is helpful to switch off the overhead projector so that students do NOT see the graph unfold as the person moves: instead, they are asked to draw what they think the graph would look like after observing the motion, and then to compare their graph with that of another. This is an important consolidation activity.

 

Slinking and Stepping (10-15 minutes)

 

Once the class is confident, it is time to challenge them. The second graph above shows the motion of a slinky as it is suspended above the motion detector and moved up and down. Again, ask students to draw what they think the graph will look like before showing them.

 

Now, ask a student to come up and try to model the same graph using their own motion. This quickly reveals gaps in understanding: frequently, I have found that students jump up and down on the spot, trying to recreate the vertical motion of the slinky, and are surprised when the graph they want does not appear. The class learns quickly from this experience.

 

Another challenge is to try to create a “step-graph” made up of vertical and horizontal line segments. Students will attempt this by moving quickly from point to point and then pausing at each stop. They will not be able to create vertical line segments that way. A fun way to attempt this one is to form a line of students equally spaced, and as you count down their numbers, each in turn is to drop quickly out of the way.

 

Alphabet Motion (10 minutes)

 

Finally, ask students to work in pairs to predict which letters of the alphabet (stick to capitals!) could be modeled by the motion detector. This is a surprisingly engaging activity and students will think, talk and learn while doing it. Without realizing it, we are actually planting the seeds here for a later study of the most important building blocks in mathematics: functions!

 

 

 

 

 

4. NUMBER: Curious Numbers

 

The Number Curiosities App displays the numbers from 0 to 25 at the top of the screen on a number line. Students may use the arrow keys to move backwards and forward along this number line, and so may use the App to support addition and subtraction activities.

 

Linked to the five blue “soft keys” below the graphing screen are menu options, which allow the user to explore different properties of each number.

 

1. X = : The first menu option allows the user to move quickly to any number by entering it (if it is a single digit number, press ENTER; if a two-digit number the app will move directly to that value after entering the second digit).

 

 

2. FAC: This option displays the factors of the number if it is composite (as shown above). If the number is prime, it simply displays the word “Prime”.

 

3. GEOM: Geometric properties of each number are a source of interest explored by the third menu option.

 

4. NUM: This option displays number relationships associated with the chosen number. There is also an invitation to investigate such properties further. In the case of the number 11, for example, the properties of palindromic numbers are explained and explored over several pages of information and questions.

 

5. WOW: This one is just for fun, linking the number to some real-world application (e.g. There are 11 players on the field during soccer and football games).

Order and Disorder

 

 

AIM                      To build student understanding of the number line as a tool for representing, ordering and for operating upon numbers.

 

METHOD            Physical involvement remains one of the most powerful tools for learning, especially in cognitive areas such as mathematics. This activity engages students in ordering and operations activities, which will be remembered for a long time because they were involved in a physical way.

 

 

PROCESS:     Stage 1: Ordering (Up to 10 minutes)

 

1. Allocate numbers from 0 on to each student in the class. This may be done using prepared cards, or by some other method.

2. Have your students form a continuous line in numerical order(this may need to be done outside the classroom!)

If you are brave, you might ask that this be done without speaking and without letting anyone else know your number!

3. Once they are settled, have them all sit down. Ask then that each in turn calls out their number (and make any necessary adjustments!)

4. Ask students to stand if they are less than 10. Sit down.

Greater than 5. Sit down.

Stand up if you just stood up for both of those questions. Explain in your own words why.

 

Continue this exercise until you are satisfied that all students are comfortable with ordering whole numbers.

 

Stage 2: Addition and Subtraction (10 minutes)

 

1.                  For this activity, use a ball or some other visible object that students will pass from one to the other. You may even like to take the last few students and make them “movers”.

2.                  The rules are simple: the ball or mover always begins at 0. As the mover passes a number, that person calls that number out. The person where the mover stops must stand up.

 

Begin with a question such as 2 + 3.

If necessary, explain that the mover begins at 0 and moves two places to the right (“0”, “1” and “2” call out their numbers). Plus 3 signals that the mover continues another 3 places to the right (“3”, “4” and “5” are called out). The person representing the number “5” stands up.

 

3.                  Continue to ask simple addition and subtraction questions until you are satisfied that students are comfortable with the process.

4.                  If you are brave and your students are ready, try re-allocating the zero position to someone else in the middle. Continue the game as students work out their new positions relative to the zero person. Do this several times.

 

Stage 3: Number Properties (10 minutes)

 

1.      Reallocate the zero person back to the start, and have students use their graphic calculators to run the Number Curiosities App. For classes with more than 25 students, ask the numbers greater than 25 to choose their favourite number and to go and sit with the person in that position.

2.      Have each student press the FAC key and move to his or her number. Have all the PRIME numbers stand up. Ask for observations from the class. Ask the prime numbers how they feel? (Special, perhaps?) Ask if there are any COMPOSITES with more than 3 factors. Who has the most factors?  What about repeated factors: the same number over and over? Whose factors can be divided equally in two? What is special about these numbers? Continue if you wish (You may want to talk about abundant numbers, with lots of factors – such as 12, where 1 + 2 + 3 + 4 + 6 > 12, and deficient numbers, with few factors – such as 9, where 1 + 3 < 9. Even consider perfect numbers, such as 6, where 1 + 2 + 3 = 6!)

3.      Now have each student press the GEOM key and ask all the odd numbers to stand up. How do they feel, being odd? Ask all the perfect squares to stand up. What was special about their factors? What about the triangular numbers? What is the pattern here?

4.      Have students compare notes with those around them. Use the app to find out other interesting things about their number.

 

 

EXTENSION and ASSESSMENT

 

      On returning to class, students should record what they have observed and learned from this exercise. This form of simple journal-keeping should be a regular part of their mathematics lessons, reflecting on what they learned, what they most enjoyed, how they might have learned more.

 

      Assessment: Prepare a report on your favourite number, recording as much as you can about that number and what makes it interesting.

 

      Alternative Task 1: Prepare a class debate: That even numbers are more interesting than odd numbers.

     

      Alternative Task 2: Complete each of the Number Curiosities headings for the numbers from 26 to 30. Make this a research assignment which may be completed individually or in groups.